Persamaan garis dapat dinyatakan dalam aneka ragam bentuk, sebagaimana telah saya tuliskan di post saya sebelumnya. Salah satu bentuk persamaan garis adalah dalam bentuk persamaan normal Hesse, yang memiliki bentuk umum:
x cos θ + y sin θ = n
Pada persamaan normal Hesse, n adalah jarak antara titik pangkal koordinat dengan garis tersebut; θ adalah sudut antara sumbu x positif dengan garis yang melalui titik pangkal koordinat dan tegak lurus terhadap garis yang menjadi perhatian kita. (Lihat Gambar 1 beserta keterangannya.)
Gambar 1
Penjelasan
Pada Gambar 1, garis hitam memiliki persamaan x cos θ + y sin θ = n. Garis berwarna merah tegak lurus garis hitam dan melalui O (titik pangkal koordinat). A adalah titik potong garis hitam dengan sumbu x positif, B adalah titik potong antara garis merah dengan garis hitam. Dengan demikian n adalah jarak antara O dengan garis hitam. Misalkan θ = ∠AOB. Jadi θ adalah sudut antara garis merah dengan sumbu x positif.
Jika suatu garis dinyatakan dalam persamaan normal Hesse, ada suatu kemudahan di dalam mencari persamaan garis hasil rotasi garis tersebut terhadap O dengan sudut rotasi φ.
Misalkan garis g memiliki persamaan x cos θ + y sin θ = n. Misalkan garis h adalah hasil rotasi g terhadap O dengan sudut rotasi φ. Maka persamaan garis h adalah x cos (θ+φ) + y sin (θ+φ) = n.
Contoh 1
Misalkan g suatu garis dengan persamaan x cos 450 + y cos 450 = 2√2. Seandainya g dirotasikan terhadap O dengan sudut rotasi 300 (berlawanan arah gerak jarum jam), maka garis hasil rotasinya, misalnya garis h, memiliki persamaan x cos 750 + y sin 750 = 2√2. (Lihat Gambar 2.)
Gambar 2
Yang menjadi pertanyaan sekarang adalah sebagai berikut. Tidak semua garis memiliki persamaan dalam bentuk normal Hesse. Bagaimana apabila persamaan garis tersebut dalam bentuk Ax + By + C = 0? Sebagai contoh, bagaimana persamaan garis hasil rotasi 2x – 9y + 9 = 0 terhadap O dengan sudut rotasi φ di mana sin φ = 0,6 dan φ sudut lancip? Hanya dengan tiga langkah mudah.
Langkah 1
Ubah bentuk Ax + By + C = 0 ke dalam bentuk persamaan normal Hesse. Sebagaimana telah dibahas pada post saya sebelumnya, persamaan normal Hesse dari persamaan tersebut adalah:
………………………………………………. (1)
Pada bagian penyebut ruas kiri (1), ada tanda ±. Pilihlah tanda positif (+) apabila C < 0 dan pilihlah tanda negatif (-) apabila C > 0.
Ubah bentuk ini ke dalam bentuk:
, dengan
(Jika pemilihan tanda aljabar penyebut ruas kiri (1) benar, nilai n yang didapat di sini pasti positif. Ingat bahwa n adalah jarak garis terhadap O, sehingga tidak boleh negatif.)
Langkah 2
Dari koefisien x, kita peroleh cos θ dan dari koefisien y, kita peroleh sin θ. Jika garis semula dirotasikan terhadap O dengan sudut rotasi φ, hitunglah cos φ dan sin φ. Karena cos θ, sin θ, cos φ, dan sin φ sudah diperoleh, nilai cos (θ+φ) dan sin (θ+φ) dapat dihitung dengan identitas-identitas trigonometri berikut.
cos (θ+φ) = cos θ cos φ – sin θ sin φ
sin (θ+φ) = sin θ cos φ + cos θ sin φ
Langkah 3
Substitusikan cos (θ+φ) dan sin (θ+φ) yang telah diperoleh pada Langkah 2 ke dalam persamaan garis hasil rotasi, yaitu:
x cos (θ+φ) + y sin (θ+φ) = n …………………………………………………………………………….. (2)
(n pada persamaan (2) tidak lain merupakan n yang diperoleh pada Langkah 1.)
Contoh 2
Diketahui garis g dengan persamaan 2x – 9y + 9 = 0. Garis ini dirotasikan terhadap O dengan sudut rotasi φ di mana sin φ = ⅗, sudut φ lancip. Tentukan persamaan garis h, yaitu hasil rotasi g tersebut.
Langkah 1
Pada kasus ini, A = 2, B = -9, dan C = 9. Karena C > 0, sebagai penyebut ruas kiri (1) kita pilih , sehingga diperoleh persamaan normal Hesse berikut:
Ubah bentuk tersebut ke dalam bentuk x cos θ + y sin θ = n, diperoleh:
Jadi, [latetx]\cos{\theta} = – \frac{2}{\sqrt{85}}[/latex], , dan .
Langkah 2
Dari sin φ = ⅗ dan φ sudut lancip, dapat diperoleh cos φ = ⅘. Dari Langkah 1, dan . Dari rumus-rumus identitas trigonometri, diperoleh:
Langkah 3
Substitusikan hasil-hasil pada Langkah 2 ke dalam x cos (θ+φ) + y sin (θ+φ) = n, dengan (hasil pada Langkah 1).
ROTASI GARIS DENGAN PERSAMAAN NORMAL HESSE
Persamaan garis dapat dinyatakan dalam aneka ragam bentuk, sebagaimana telah saya tuliskan di post saya sebelumnya. Salah satu bentuk persamaan garis adalah dalam bentuk persamaan normal Hesse, yang memiliki bentuk umum:
x cos θ + y sin θ = n
Pada persamaan normal Hesse, n adalah jarak antara titik pangkal koordinat dengan garis tersebut; θ adalah sudut antara sumbu x positif dengan garis yang melalui titik pangkal koordinat dan tegak lurus terhadap garis yang menjadi perhatian kita. (Lihat Gambar 1 beserta keterangannya.)
Gambar 1
Penjelasan
Pada Gambar 1, garis hitam memiliki persamaan x cos θ + y sin θ = n. Garis berwarna merah tegak lurus garis hitam dan melalui O (titik pangkal koordinat). A adalah titik potong garis hitam dengan sumbu x positif, B adalah titik potong antara garis merah dengan garis hitam. Dengan demikian n adalah jarak antara O dengan garis hitam. Misalkan θ = ∠AOB. Jadi θ adalah sudut antara garis merah dengan sumbu x positif.
Jika suatu garis dinyatakan dalam persamaan normal Hesse, ada suatu kemudahan di dalam mencari persamaan garis hasil rotasi garis tersebut terhadap O dengan sudut rotasi φ.
Misalkan garis g memiliki persamaan x cos θ + y sin θ = n. Misalkan garis h adalah hasil rotasi g terhadap O dengan sudut rotasi φ. Maka persamaan garis h adalah x cos (θ+φ) + y sin (θ+φ) = n.
Contoh 1
Misalkan g suatu garis dengan persamaan x cos 450 + y cos 450 = 2√2. Seandainya g dirotasikan terhadap O dengan sudut rotasi 300 (berlawanan arah gerak jarum jam), maka garis hasil rotasinya, misalnya garis h, memiliki persamaan x cos 750 + y sin 750 = 2√2. (Lihat Gambar 2.)
Gambar 2
Yang menjadi pertanyaan sekarang adalah sebagai berikut. Tidak semua garis memiliki persamaan dalam bentuk normal Hesse. Bagaimana apabila persamaan garis tersebut dalam bentuk Ax + By + C = 0? Sebagai contoh, bagaimana persamaan garis hasil rotasi 2x – 9y + 9 = 0 terhadap O dengan sudut rotasi φ di mana sin φ = 0,6 dan φ sudut lancip? Hanya dengan tiga langkah mudah.
Langkah 1
Ubah bentuk Ax + By + C = 0 ke dalam bentuk persamaan normal Hesse. Sebagaimana telah dibahas pada post saya sebelumnya, persamaan normal Hesse dari persamaan tersebut adalah:
Pada bagian penyebut ruas kiri (1), ada tanda ±. Pilihlah tanda positif (+) apabila C < 0 dan pilihlah tanda negatif (-) apabila C > 0.
Ubah bentuk ini ke dalam bentuk:
(Jika pemilihan tanda aljabar penyebut ruas kiri (1) benar, nilai n yang didapat di sini pasti positif. Ingat bahwa n adalah jarak garis terhadap O, sehingga tidak boleh negatif.)
Langkah 2
Dari koefisien x, kita peroleh cos θ dan dari koefisien y, kita peroleh sin θ. Jika garis semula dirotasikan terhadap O dengan sudut rotasi φ, hitunglah cos φ dan sin φ. Karena cos θ, sin θ, cos φ, dan sin φ sudah diperoleh, nilai cos (θ+φ) dan sin (θ+φ) dapat dihitung dengan identitas-identitas trigonometri berikut.
cos (θ+φ) = cos θ cos φ – sin θ sin φ
sin (θ+φ) = sin θ cos φ + cos θ sin φ
Langkah 3
Substitusikan cos (θ+φ) dan sin (θ+φ) yang telah diperoleh pada Langkah 2 ke dalam persamaan garis hasil rotasi, yaitu:
x cos (θ+φ) + y sin (θ+φ) = n …………………………………………………………………………….. (2)
(n pada persamaan (2) tidak lain merupakan n yang diperoleh pada Langkah 1.)
Contoh 2
Diketahui garis g dengan persamaan 2x – 9y + 9 = 0. Garis ini dirotasikan terhadap O dengan sudut rotasi φ di mana sin φ = ⅗, sudut φ lancip. Tentukan persamaan garis h, yaitu hasil rotasi g tersebut.
Langkah 1
Pada kasus ini, A = 2, B = -9, dan C = 9. Karena C > 0, sebagai penyebut ruas kiri (1) kita pilih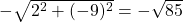 , sehingga diperoleh persamaan normal Hesse berikut:
, sehingga diperoleh persamaan normal Hesse berikut:
Ubah bentuk tersebut ke dalam bentuk x cos θ + y sin θ = n, diperoleh:
Jadi, [latetx]\cos{\theta} = – \frac{2}{\sqrt{85}}[/latex],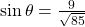 , dan
, dan  .
.
Langkah 2
Dari sin φ = ⅗ dan φ sudut lancip, dapat diperoleh cos φ = ⅘. Dari Langkah 1,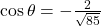 dan
dan 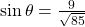 . Dari rumus-rumus identitas trigonometri, diperoleh:
. Dari rumus-rumus identitas trigonometri, diperoleh:
Langkah 3
Substitusikan hasil-hasil pada Langkah 2 ke dalam x cos (θ+φ) + y sin (θ+φ) = n, dengan (hasil pada Langkah 1).
(hasil pada Langkah 1).
– 7x + 6y = 9 (persamaan garis h)
Lihat juga materi serupa ini:
Rotasi dan Translasi Elips
Rotasi dan Translasi Hiperbola
Rotasi Hiperbola Ortogonal
Translasi dan Rotasi Parabola
Bagikan ini:
Most visitors also read :
BERKENALAN DENGAN NILAI DAN VEKTOR EIGEN
DEKOMPOSISI NILAI SINGULAR (SINGULAR VALUE DECOMPOSITION)
MATRIKS AKAR KUADRAT
SOAL DAN PEMBAHASAN ANALISIS KOMPONEN UTAMA