Istilah akar kuadrat sudah biasa kita temukan sejak tingkat sekolah dasar. Namun akar kuadrat yang dimaksud di sini adalah akar kuadrat dari suatu bilangan nyata tak negatif.
Satu hal yang sering disalahartikan namun ada hubungannya dengan akar kuadrat adalah penyelesaian dari suatu persamaan kuadrat. Sebagai contoh, persamaan kuadrat x2 = 16 memiliki dua buah penyelesaian riil, yaitu atau . Berbeda dengan akar kuadrat suatu bilangan nyata: akar kuadrat dari suatu bilangan nyata tak negatif selalu tidak negatif. Secara matematis dapat dituliskan untuk setiap .
Sekarang, bagaimana apabila ditemukan “persamaan kuadrat” dalam matriks? Sebagai contoh, misalnya . Matriks X yang memenuhi persamaan X2 = B (atau X.X =B) , apabila persamaan ini memiliki solusi, dinamakan matriks akar kuadrat. Penyelesaian bagi X2 = B, apabila ada, dilambangkan dengan B1/2.
Bagaimana cara menentukan matriks akar kuadrat tersebut? Perhatikan uraian berikut ini.
Misalkan A adalah suatu matriks definit positif dengan dekomposisi spektral sebagai berikut.
dengan adalah pasangan-pasangan nilai eigen – vektor eigen yang semua vektor eigennya yang bernorma satu dan saling tegak lurus. Dengan mendefinisikan matriks dan matriks di mana , dekomposisi tersebut dapat juga dinyatakan sebagai:
Matriks yang didefinisikan sebagai merupakan suatu solusi persamaan matriks X2 = A. (Dengan kata lain, A1/2.A1/2 = A.) Selanjutnya, jika kita definisikan matriks dengan maka A1/2 dapat juga dinyatakan sebagai:
Beberapa sifat matriks akar kuadrat di atas adalah sebagai berikut.
A1/2 merupakan suatu matriks simetris.
Invers matriks A1/2, yaitu dan dilambangkan dengan A-1/2, adalah: dengan di mana .
Kuadrat dari A-1/2 merupakan invers matriks A. Dengan kata lain, A-1/2.A-1/2 = A-1.
Contoh Soal
Diketahui matriks definit positif . Tentukan A1/2, A-1/2, dan A-1.
Jawab
Nilai-nilai eigen dari A adalah λ1 = 6 dan λ2 = 1. Untuk λ1 = 6, diperoleh dan untuk λ2 = 1 diperoleh . Dari , λ1, dan λ2 tersebut diperoleh matriks , , dan dekomposisi spektral sebagai berikut.
Untuk menentukan A1/2, tentukan terlebih dahulu Λ-1/2, yaitu . Selanjutnya diperoleh:
Untuk menentukan A-1, kita dapat juga menggunakan rumus yang telah diuraikan sebelumnya:
A-1/2 . A-1/2 = A-1
Jadi,
Catatan Penyerta A-1
Tentu ada cara lain untuk menentukan A-1, namun di pembahasan ini sengaja digunakan di samping cara lain, sekedar untuk mendemonstrasikan rumus tersebut. Selanjutnya, jika A memiliki dekomposisi spektral A = PΛP’, inversnya dapat pula dinyatakan sebagai A = PΛ-1P’ atau dengan , di mana .
Jika A-1 pada contoh soal di atas dikerjakan dengan cara lain tersebut, maka dan selanjutnya diperoleh:
MATRIKS AKAR KUADRAT
Istilah akar kuadrat sudah biasa kita temukan sejak tingkat sekolah dasar. Namun akar kuadrat yang dimaksud di sini adalah akar kuadrat dari suatu bilangan nyata tak negatif.
Satu hal yang sering disalahartikan namun ada hubungannya dengan akar kuadrat adalah penyelesaian dari suatu persamaan kuadrat. Sebagai contoh, persamaan kuadrat x2 = 16 memiliki dua buah penyelesaian riil, yaitu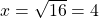 atau
atau  . Berbeda dengan akar kuadrat suatu bilangan nyata: akar kuadrat dari suatu bilangan nyata tak negatif selalu tidak negatif. Secara matematis dapat dituliskan
. Berbeda dengan akar kuadrat suatu bilangan nyata: akar kuadrat dari suatu bilangan nyata tak negatif selalu tidak negatif. Secara matematis dapat dituliskan  untuk setiap
untuk setiap  .
.
Sekarang, bagaimana apabila ditemukan “persamaan kuadrat” dalam matriks? Sebagai contoh, misalnya . Matriks X yang memenuhi persamaan X2 = B (atau X.X =B) , apabila persamaan ini memiliki solusi, dinamakan matriks akar kuadrat. Penyelesaian bagi X2 = B, apabila ada, dilambangkan dengan B1/2.
. Matriks X yang memenuhi persamaan X2 = B (atau X.X =B) , apabila persamaan ini memiliki solusi, dinamakan matriks akar kuadrat. Penyelesaian bagi X2 = B, apabila ada, dilambangkan dengan B1/2.
Bagaimana cara menentukan matriks akar kuadrat tersebut? Perhatikan uraian berikut ini.
Misalkan A adalah suatu matriks definit positif dengan dekomposisi spektral sebagai berikut.
dengan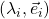 adalah pasangan-pasangan nilai eigen – vektor eigen yang semua vektor eigennya yang bernorma satu dan saling tegak lurus. Dengan mendefinisikan matriks
adalah pasangan-pasangan nilai eigen – vektor eigen yang semua vektor eigennya yang bernorma satu dan saling tegak lurus. Dengan mendefinisikan matriks  dan matriks
dan matriks ![Rendered by QuickLaTeX.com \Lambda = [\lambda_{ij}]](http://edscyclopedia.com/wp-content/ql-cache/quicklatex.com-34a8b6bbd49ce0bfe7872a7188bb3df6_l3.png) di mana
di mana  , dekomposisi tersebut dapat juga dinyatakan sebagai:
, dekomposisi tersebut dapat juga dinyatakan sebagai:
Matriks yang didefinisikan sebagai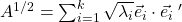 merupakan suatu solusi persamaan matriks X2 = A. (Dengan kata lain, A1/2.A1/2 = A.) Selanjutnya, jika kita definisikan matriks
merupakan suatu solusi persamaan matriks X2 = A. (Dengan kata lain, A1/2.A1/2 = A.) Selanjutnya, jika kita definisikan matriks ![Rendered by QuickLaTeX.com \Lambda^{1/2}= [l_{ij}]](http://edscyclopedia.com/wp-content/ql-cache/quicklatex.com-783048f3bea488253431fa2efeaa1539_l3.png) dengan
dengan  maka A1/2 dapat juga dinyatakan sebagai:
maka A1/2 dapat juga dinyatakan sebagai:
Beberapa sifat matriks akar kuadrat di atas adalah sebagai berikut.
Contoh Soal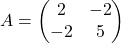 . Tentukan A1/2, A-1/2, dan A-1.
. Tentukan A1/2, A-1/2, dan A-1.
Diketahui matriks definit positif
Jawab dan untuk λ2 = 1 diperoleh
dan untuk λ2 = 1 diperoleh  . Dari
. Dari  , λ1, dan λ2 tersebut diperoleh matriks
, λ1, dan λ2 tersebut diperoleh matriks 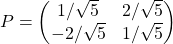 ,
, 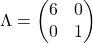 , dan dekomposisi spektral sebagai berikut.
, dan dekomposisi spektral sebagai berikut.
Nilai-nilai eigen dari A adalah λ1 = 6 dan λ2 = 1. Untuk λ1 = 6, diperoleh
Untuk menentukan A1/2, tentukan terlebih dahulu Λ-1/2, yaitu . Selanjutnya diperoleh:
. Selanjutnya diperoleh:
Untuk menentukan A-1, kita dapat juga menggunakan rumus yang telah diuraikan sebelumnya:
A-1/2 . A-1/2 = A-1
Jadi,
Catatan Penyerta A-1
Tentu ada cara lain untuk menentukan A-1, namun di pembahasan ini sengaja digunakan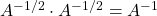 di samping cara lain, sekedar untuk mendemonstrasikan rumus tersebut. Selanjutnya, jika A memiliki dekomposisi spektral A = PΛP’, inversnya dapat pula dinyatakan sebagai A = PΛ-1P’ atau
di samping cara lain, sekedar untuk mendemonstrasikan rumus tersebut. Selanjutnya, jika A memiliki dekomposisi spektral A = PΛP’, inversnya dapat pula dinyatakan sebagai A = PΛ-1P’ atau  dengan
dengan ![Rendered by QuickLaTeX.com \Lambda^{-1}=[l_{ij}]](http://edscyclopedia.com/wp-content/ql-cache/quicklatex.com-602d072e793d677942dffa540fd24593_l3.png) , di mana
, di mana  .
.
Jika A-1 pada contoh soal di atas dikerjakan dengan cara lain tersebut, maka dan selanjutnya diperoleh:
dan selanjutnya diperoleh:
Bagikan ini:
Most visitors also read :
BERKENALAN DENGAN NILAI DAN VEKTOR EIGEN
DEKOMPOSISI NILAI SINGULAR (SINGULAR VALUE DECOMPOSITION)
SOAL DAN PEMBAHASAN ANALISIS KOMPONEN UTAMA
DEKOMPOSISI SPEKTRAL MATRIKS SIMETRIS