TITIK BERAT SEGITIGA

(English version of this article is available at edsmathscholar.com, click here)
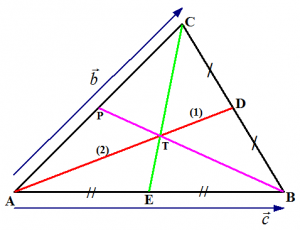
Diketahui ∆ABC sembarang. Untuk menentukan titik berat segitiga itu, buat garis pertama yang melewati salah satu titik sudutnya (misalnya A) dan titik tengah sisi yang di hadapannya (yaitu titik tengah BC, misalnya titik D). Buat garis kedua yang melewati titik sudut lainnya (misalnya C) dan titik tengah sisi yang di hadapannya (yaitu titik tengah AB, misalnya titik E). Misalkan T adalah titik potong kedua garis tersebut. T adalah titik berat ∆ABC.

Berapakah AT:TD? Berapakah CT:TE? Kita akan menjawab itu.
Misalkan:
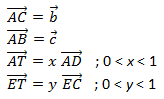
Perhatikan bahwa:
![]()
Dari pemisalan-pemisalan di atas, diperoleh:

Karena
![]()
persamaan di atas dapat dituliskan sbb.:
![]()
Dari persamaan terakhir ini diperoleh x = 2/3 dan y = 1/3.
Jadi, AT:TD = CT:TE = 2:1.
Sekarang, seandainya ditarik suatu garis ketiga yang melalui titik sudut B dan titik tengah AC, apakah garis itu akan melalui T (= titik berat ∆ABC)? Dengan kata lain, apakah semua garis berat berpotongan di satu titik? Ya! Mari kita buktikan. Misalkan titik tengah AC adalah P.

Perhatikan bahwa
![]()
Ternyata:
![]()
Hasil terakhir ini menunjukkan dua hal. Pertama: titik B, P, dan T terletak pada satu garis, dan kedua: BT:BP = 2:1. Jadi, ketiga garis berat ∆ABC berpotongan di satu titik, yaitu titik T.
Pertanyaan selanjutnya sekarang: Apabila koordinat A, B, dan C dalam ∆ABC tersebut diketahui, bagaimana cara menentukan koordinat titik berat segitiga tersebut? Dari hasil sebelumnya telah diperoleh bahwa:
![]()
Dengan notasi vektor posisi, persamaan ini dapat ditulis kembali sebagai berikut.

Karena E adalah titik tengah ruas garis AB,

Dengan demikian koordinat titik berat ∆ABC dengan mudah dapat disimpulkan dari vektor posisi T.
Contoh 1:
Diketahui ∆ABC dengan A(1,5), B(-3,8), dan C(5,11). Tentukan koordinat titik berat ∆ABC!
Jawab:
Misalkan titik berat ∆ABC adalah T.
![]()
Jadi, koordinat titik berat ∆ABC adalah (1,8).
Contoh 2:
Diketahui ∆ABC dengan A(1,5,0), B(-3,8,4), dan C(5,11,2). Tentukan koordinat titik berat ∆ABC!
Jawab:
Misalkan titik berat ∆ABC adalah T.
![]()
Jadi, koordinat titik berat ∆ABC adalah (1,8,2).
Berapakah jarak antara titik berat suatu segitiga terhadap alas segitiga tersebut? Perhatikan ∆ABC di bawah ini.

Pada segitiga tersebut, AD dan CE adalah garis-garis berat ∆ABC dengan T sebagai titik beratnya. Dari hasil sebelumnya diperoleh bahwa CT:TE = 2:1. Pada ∆ABC, K adalah suatu titik pada AB sedemikian hingga CK ⊥ AB (CK adalah garis tinggi yang ditarik dari C) dan L adalah suatu titik pada AB sedemikian hingga TL ⊥ AB. Perhatikan bahwa ∆CKE sebangun dengan ∆TLE sehingga:
![]()
Dari perbandingan CT:TE, diperoleh bahwa CE = 3 TE dan selanjutnya diperoleh:
![]()
Jadi, jarak titik berat suatu segitiga dari suatu alas segitiga itu adalah sepertiga dari tinggi yang didirikan di atas alas tersebut.
Hal-hal lain menyangkut segitiga:
Beragam cara menghitung luas segitiga
Sudut istimewa lain dalam segitiga
Tagging: centroid, centroid of a triangle, garis berat, median, titik berat




Mantaps, makasih 🙂
Good… terimakasih.
Mas, mau tanya sedikit.
Di kalimat “Dari persamaan terakhir ini diperoleh x = 2/3 dan y = 1/3”
Saya masih tidak mengerti prosesnya.
Darimana diperoleh nilai x=2/3 dan y=1/3.
Sebab di atas, tidak disertakan perhitungan detailnya.
Terimakasih sebelumnya bila bersedia menjawab pertanyaan saya 🙂
Bisa minta alamat e-mail-nya? Terima kasih.
mas bagaimana persamaannya bisa seperti itu?
Persamaan yang mana? Bisa seperti itu bagaimana maksudnya?
Mas, saya ingin bertanya hal yang sama
Di kalimat “Dari persamaan terakhir ini diperoleh x = 2/3 dan y = 1/3”
Saya masih tidak mengerti prosesnya.
Darimana diperoleh nilai x=2/3 dan y=1/3.
Sebab di atas, tidak disertakan perhitungan detailnya.
Memangnya titik berat selalu ada pada tengah-tengah segitiga, ya?
Berarti gk boleh langsung dibagi 3. ( yang 3 dimensi)
Makasiiii ^^
makasih kak
kok bisa langsung disapat persamaan akhirnya begitu yaa?
X=2/3 itu dr mana ya?