ROTASI HIPERBOLA ORTOGONAL

Diketahui suatu hiperbola dengan persamaan xy = 2. Berapakah koordinat titik fokus dan bagaimanakah persamaan garis direktriks serta garis-garis asimtotnya? Dalam post kali ini, akan diuraikan rumus cepatnya.
Rumus cepat:
Jika diketahui hiperbola dengan persamaan xy = k dengan k > 0 maka:
- Koordinat titik-titik fokus: [pmath](sqrt{2k},sqrt{2k})[/pmath] dan [pmath](-~sqrt{2k},~-~sqrt{2k})[/pmath]
- Persamaan garis direktriks: [pmath]y ~=~ – ~x ~+~sqrt{2k}[/pmath] dan [pmath]y ~=~ – ~x ~-~sqrt{2k}[/pmath]
- Persamaan garis asimtot: x = 0 (sumbu y) dan y = 0 (sumbu x)
Dengan demikian pertanyaan tadi dapat dijawab dengan mudah. Dengan mensubstitusikan k = 2 ke dalam rumus cepat di atas, diperoleh koordinat titik-titik fokusnya adalah (2,2) dan (-2,-2), persamaan garis direktriksnya adalah y = –x + 2 dan y = –x – 2. Persamaan garis asimtotnya adalah y = 0 dan x = 0. (Lihat gambar di bawah.)

Mudah-mudahan rumus cepat di atas bisa membantu adik-adik dalam menyelesaikan masalah serupa itu. TETAPI … Hanya mengetahui rumus cepat saja sangat tidak baik! Kita harus mengetahui bagaimana landasan pemikiran sehingga diperoleh rumus tersebut. Mari kita lihat “dapur” pembuatan rumus tersebut. Simaklah uraian di bawah ini.
Adik-adik SMA jurusan IPA tentu sudah mengenal persamaan umum hiperbola [pmath]{x^2}/{a^2} ~-~ {y^2}/{b^2} ~=~ 1[/pmath] (hiperbola horizontal) dan [pmath]{y^2}/{a^2} ~-~ {x^2}/{b^2} ~=~ 1[/pmath] (hiperbola vertikal). Dengan diketahui nilai a dan b persamaan-persamaan itu dengan mudah kita dapat mengetahui koordinat titik fokus, koordinat titik potong dengan sumbu x atau sumbu y, persamaan garis direktris, persamaan garis asimtot, panjang latus rectum, dan sebagainya.
Ada baiknya berikut ini diringkaskan rumus-rumus berkenaan dengan persamaan hiperbola tersebut.
HIPERBOLA HORIZONTAL
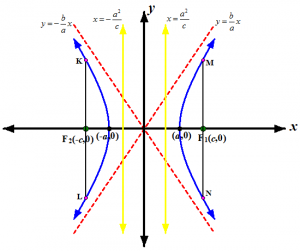
Gambar 1
Hiperbola Horizontal
Persamaan : [pmath]{x^2}/{a^2} ~-~ {y^2}/{b^2} ~=~ 1[/pmath]
Pusat : O(0,0)
Fokus-fokus : F1(c,0) dan F2(-c,0)
Titik potong dengan sumbu x : (a,0) dan (-a,0)
Persamaan garis direktriks : [pmath]x ~=~ pm {a^2}/c[/pmath]
Persamaan garis asimtot : [pmath]y ~=~ pm {b/a} x[/pmath]
Latus rectum : [pmath]delim{|}{overline{KL}}{|}=delim{|}{overline{MN}}{|}={2b^2}/a[/pmath]
Eksentrisitas : [pmath]e ~=~ c/a[/pmath]
Catatan:
- Pada rumus-rumus di atas a, b, c > 0
- Berlaku hubungan [pmath]b^2 ~=~ c^2 ~-~ a^2[/pmath]
HIPERBOLA VERTIKAL
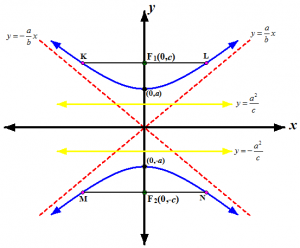
Gambar 2
Hiperbola Vertikal
Persamaan : [pmath]{y^2}/{a^2} ~-~ {x^2}/{b^2} ~=~ 1[/pmath]
Pusat : O(0,0)
Fokus-fokus : F1(0,c) dan F2(0,-c)
Titik potong dengan sumbu y : (0,a) dan (0,-a)
Persamaan garis direktriks : [pmath]y ~=~ pm {a^2}/c[/pmath]
Persamaan garis asimtot : [pmath]y ~=~ pm {a/b} x[/pmath]
Latus rectum : [pmath]delim{|}{overline{KL}}{|}=delim{|}{overline{MN}}{|}={2b^2}/a[/pmath]
Eksentrisitas : [pmath]e ~=~ c/a[/pmath]
Catatan:
- Pada rumus-rumus di atas a, b, c > 0
- Berlaku hubungan [pmath]b^2 ~=~ c^2 ~-~ a^2[/pmath]
HIPERBOLA ORTOGONAL
Pada persamaan-persamaan hiperbola di atas, apabila a = b, kurva yang terbentuk dinamakan hiperbola ortogonal. Jadi, terdapat dua macam hiperbola ortogonal, yaitu yang horizontal dan yang vertikal. Hiperbola horizontal memiliki persamaan x2 – y2 = a2 dan yang vertikal memiliki persamaan y2 – x2 = a2. Pada hiperbola ortogonal, garis-garis asimtot saling tegak lurus (= ortogonal) satu sama lain. Persamaan garis-garis asimtot tersebut adalah y = x dan y = –x. (Lihat gambar di bawah.)

Gambar 3
Hiperbola Ortogonal Horizontal
ROTASI HIPERBOLA ORTOGONAL SEBANYAK 450 TERHADAP O
Misalkan diketahui suatu hiperbola ortogonal dengan persamaan x2 – y2 = a2. Apa yang terjadi ketika hiperbola ini dirotasikan 450 terhadap O? Setiap titik yang berkoordinat (x,y) akan berpindah ke titik berkoordinat (x’,y’) dengan:
[pmath]x prime ~=~ x/{sqrt{2}} ~-~ y/{sqrt{2}}[/pmath] …………………………………………….. (1)
[pmath]y prime ~=~ x/{sqrt{2}} ~+~ y/sqrt{2}[/pmath] ……………………………………………… (2)
Dengan teknik penyelesaikan sistem persamaan linier, dari (1) dan (2) diperoleh:
[pmath]x ~=~ {x prime}/{sqrt{2}} ~+~ {y prime}/{sqrt{2}}[/pmath] ………………………………. (1*)
[pmath]y ~=~ {- x prime}/{sqrt{2}} ~+~ {y prime}/{sqrt{2}}[/pmath] …………………………….. (2*)
Substitusikan (1*) dan (2*) ini ke persamaan semula x2 – y2 = a2, akan diperoleh persamaan:
[pmath]{x prime}{y prime} ~=~ {a^2}/2[/pmath] ……………………………………………………….. (3)
Dengan memperhatikan keterkaitan antara persamaan semula x2 – y2 = a2 dengan (3) diperoleh bahwa hasil rotasi hiperbola x2 – y2 = a2 sebanyak 450 terhadap O menghasilkan hiperbola dengan bentuk umum persamaan:
[pmath]xy ~=~ k[/pmath] dengan [pmath]k ~=~ {a^2}/2[/pmath] dan k > 0.
Sekarang, bagaimana dengan titik-titik fokus, garis direktriks, dan garis asimtot hiperbola dengan persamaan x2 – y2 = k dengan k > 0? Dengan diketahuinya hubungan antara (3) dan persamaan semula x2 – y2 = a2 pertanyaan ini dapat dijawab. Dengan diketahuinya hubungan tersebut, kita dapat menentukan fokus, garis direktriks, dan garis asimtot sebelum hiperbola tersebut dirotasikan. Dengan kata lain, kita menelusuri kembali keadaan hiperbola (sekaligus beserta titik-titik fokus, garis direktriks, dan garis asimtotnya) sebelum hiperbola diputar.
Menentukan Fokus Hiperbola xy = k
Karena [pmath]k ~=~ {a^2}/2[/pmath], a2 = b2 = 2k. Substitusikan ini ke dalam b2 = c2 – a2, akhirnya diperoleh [pmath]c ~=~ pm 2 sqrt{k}[/pmath]. Jadi, sebelum dirotasikan 450, fokus-fokus hiperbola ini berkoordinat (2√k,0) dan (-2√k,0). Dengan menggunakan (1) dan (2) terhadap koordinat kedua fokus ini, diperoleh bahwa koordinat fokus-fokus hiperbola xy = k ini adalah [pmath](sqrt{2k},sqrt{2k})[/pmath] dan [pmath](-~sqrt{2k},~-~sqrt{2k})[/pmath].
Menentukan Persamaan Garis Direktriks Hiperbola xy = k
Dengan alur pikir yang serupa dengan penentuan fokus, diperoleh bahwa persamaan garis direktriks hiperbola xy = k adalah [pmath]y ~=~ – ~x ~+~sqrt{2k}[/pmath] dan [pmath]y ~=~ – ~x ~-~sqrt{2k}[/pmath].
Menentukan Persamaan Garis Asimtot Hiperbola xy = k
Sebelumnya telah diuraikan bahwa garis-garis asimtot suatu hiperbola ortogonal memiliki persamaan y = x dan y = –x. Perhatikan bahwa kedua garis ini membentuk sudut 450 dan 1350 terhadap sumbu x positif. Akibatnya jelas, apabila kedua garis ini dirotasikan 450 terhadap O maka hasil rotasinya akan berimpit dengan kedua sumbu koordinat. Jadi, garis-garis asimtot hiperbola xy = k adalah kedua sumbu koordinat.
Lihat juga materi serupa ini:
Rotasi dan Translasi Hiperbola
Rotasi Garis dengan Persamaan Normal Hesse
Tagging: hiperbola ortogonal, rotasi hiperbola



sangat membantu thankss