Pada posting saya yang lalu saya telah menguraikan mengenai perpangkatan bilangan nyata. Satu hal yang tak akan lepas hubungannya dengan perpangkatan adalah apa yang disebut dengan “pengambilan logaritma”. Tentang bagaimana hubungan tersebut dapat dilihat pada definisi berikut.
Definisi
Misalkan , a, g > 0 dan g ≠ 1. jika dan hanya jika . g dinamakan basis atau bilangan pokok logaritma, sedangkan a dinamakan numerus.
Catatan:
Jika bilangan pokok suatu logaritma tidak dituliskan, dianggap bahwa bilangan pokoknya adalah 10. Jadi, log a = 10log a. Logaritma dengan bilangan pokok 10 dinamakan logaritma dengan sistem Briggsian. Satu jenis logaritma lagi yang sering digunakan adalah logaritma dengan sistem Napierian. Logaritma ini menggunakan bilangan Eulere sebagai bilangan pokoknya. Logaritma ini mempunyai notasi yang berbeda, yaitu ln (natural logarithm, logaritma alami). Untuk setiap a > 0, ln a didefinisikan sebagai berikut: ln a = elog a.
Pada pendefinisian logaritma sebagaimana yang telah diuraikan sebelumnya, basis suatu logaritma tidak boleh bernilai 1. Mengapa? Seandainya diperbolehkan basis yang bernilai 1 akibatnya sebagai berikut. 1log 1 = 4 [karena 14 = 1] dan juga 1log 1 = 2 [karena 12 = 1]. Dari sini disimpulkan 4 = 2, suatu pernyataan yang keliru!!! Karena itu basis suatu logaritma harus positif namun tidak boleh bernilai 1.
Mari kita perhatikan kembali hubungan antara pangkat dan logaritma. Ambil satu contoh misalnya 23 = 8. Berdasarkan definisi logaritma, kita dapat menyatakan bahwa 3 = 2log 8. Substitusikan 3 = 2log 8 ini ke dalam 23 = 8, diperolehlah . Ini merupakan suatu ilustrasi penerapan Rumus 1 berikut.
Rumus 1
; a, g > 0 dan g ≠ 1
Contoh 1:
Contoh 2:
Rumus 2
; a, b, g > 0 dan g ≠ 1
Contoh 3:
Jika log 2 = 0,3010 dan log 3 = 0,4771 maka berapakah log 6?
LOGARITMA
Pada posting saya yang lalu saya telah menguraikan mengenai perpangkatan bilangan nyata. Satu hal yang tak akan lepas hubungannya dengan perpangkatan adalah apa yang disebut dengan “pengambilan logaritma”. Tentang bagaimana hubungan tersebut dapat dilihat pada definisi berikut.
Definisi
Misalkan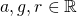 , a, g > 0 dan g ≠ 1.
, a, g > 0 dan g ≠ 1. 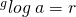 jika dan hanya jika
jika dan hanya jika  . g dinamakan basis atau bilangan pokok logaritma, sedangkan a dinamakan numerus.
. g dinamakan basis atau bilangan pokok logaritma, sedangkan a dinamakan numerus.
Catatan:
Jika bilangan pokok suatu logaritma tidak dituliskan, dianggap bahwa bilangan pokoknya adalah 10. Jadi, log a = 10log a. Logaritma dengan bilangan pokok 10 dinamakan logaritma dengan sistem Briggsian. Satu jenis logaritma lagi yang sering digunakan adalah logaritma dengan sistem Napierian. Logaritma ini menggunakan bilangan Euler e sebagai bilangan pokoknya. Logaritma ini mempunyai notasi yang berbeda, yaitu ln (natural logarithm, logaritma alami). Untuk setiap a > 0, ln a didefinisikan sebagai berikut: ln a = elog a.
Contoh-contoh:
Berapakah 2log 16? 2log 16 = 4 [karena 24 = 16]
Berapakah 5log 125? 5log 125 = 3 [karena 53 = 125]
Berapakah 3log ⅓? 3log ⅓ = -1 [karena 3-1 = ⅓]
Berapakah log 10000? log 10000 = 4 [karena 104 = 10000] (note: basis 10 tidak dituliskan dalam notasi logaritma)
Berapakan ln 1? ln 1 = 0 [karena e0 = 1] (note: ln 1 = elog 1)
Pada pendefinisian logaritma sebagaimana yang telah diuraikan sebelumnya, basis suatu logaritma tidak boleh bernilai 1. Mengapa? Seandainya diperbolehkan basis yang bernilai 1 akibatnya sebagai berikut. 1log 1 = 4 [karena 14 = 1] dan juga 1log 1 = 2 [karena 12 = 1]. Dari sini disimpulkan 4 = 2, suatu pernyataan yang keliru!!! Karena itu basis suatu logaritma harus positif namun tidak boleh bernilai 1.
Mari kita perhatikan kembali hubungan antara pangkat dan logaritma. Ambil satu contoh misalnya 23 = 8. Berdasarkan definisi logaritma, kita dapat menyatakan bahwa 3 = 2log 8. Substitusikan 3 = 2log 8 ini ke dalam 23 = 8, diperolehlah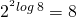 . Ini merupakan suatu ilustrasi penerapan Rumus 1 berikut.
. Ini merupakan suatu ilustrasi penerapan Rumus 1 berikut.
Rumus 1
Contoh 1:
Contoh 2:
Rumus 2
Contoh 3:
Jika log 2 = 0,3010 dan log 3 = 0,4771 maka berapakah log 6?
log 6 = log 2.3 = log 2 + log 3 =0,3010 + 0,4771 = 0,7781
Contoh 4:
Jika log 2 = 0,3010 maka berapakah log 2000?
log 2000 = log 2.1000 = log 2 + log 1000 = 0,3010 + 3 = 3,3010
Rumus 3
Contoh 5:
Jika log 2 = 0,3010 dan log 3 = 0,4771 maka berapakah log 1,5?
Contoh 6:
Jika log 2 = 0,3010 maka berapakah log 5?
Rumus 4
Contoh 7:
Jika log 3 = 0,4771 maka berapakah log 243?
log 243 = log 35 = 5.log 3 = 5.0,4771 = 2,3855
Contoh 8:
Berapakah ln e√7?
ln e√7 = (√7).ln e = √7 . 1 = √7 [Ingat mengenai logaritma natural; ln e = elog e = 1]
Contoh 9:
Berapakah ?
?
Rumus 5
Contoh 10:
Berapakah 16log 64?
Contoh 11:
Jika 2log 3 = 1,585 maka berapakah 8log 3?
Rumus 6
Dalam rumus ini, k adalah sembarang bilangan nyata dengan k > 0 dan k ≠ 1.
Contoh 12
Berapakah 16log 64?
Contoh 13
Jika 2log 3 = 1,585 maka berapakah 3log 2?
Penyelesaian pada Contoh 13 membawa ide bagi pembuktian rumus berikut.
Rumus 7
Tautan-tautan yang berkaitan dengan posting ini:
Bagikan ini:
Most visitors also read :
BERKENALAN DENGAN NILAI DAN VEKTOR EIGEN
DEKOMPOSISI NILAI SINGULAR (SINGULAR VALUE DECOMPOSITION)
MATRIKS AKAR KUADRAT
SOAL DAN PEMBAHASAN ANALISIS KOMPONEN UTAMA