PERSAMAAN GARIS (1)
Kita tentunya mengenal suatu alat tulis yang dinamakan penggaris. Penggaris adalah suatu alat tulis untuk membantu kita dalam menggambar sebuah garis. Istilah garis pun sudah tidak terdengar asing di telinga kita. Namun apakah garis itu sebenarnya? Dalam plane Euclidean geometry, garis merupakan salah satu istilah yang tidak terdefinisi (undefined term). Singkat kata, kita tidak dapat menemukan suatu definisi yang memuaskan mengenai apakah garis itu. Setiap kita mencoba mendefinisikan garis, pasti kemudian ada pertanyaan lanjutan yang tidak berkesudahan. Namun demikian, ada baiknya kita mempelajari pernyataan-pernyataan yang berkenaan dengan garis sebagai usaha atau upaya untuk mendefinisikan garis. Euclid memandang garis sebagai perluasan dari lintasan terpendek antara dua titik. Misalkan terdapat dua buah titik A dan B. Dari A, dapat dibuat tak berhingga banyaknya lintasan yang berakhir di B dan dari B dapat dibuat tak berhingga banyaknya lintasan yang berakhir di A. Namun, lintasan yang terpendek akan berupa suatu ”ruas garis” (lihat gambar di bawah).
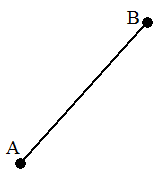
Gambar 1
Yang dimaksudkan Euclid mengenai garis adalah perluasan dari ruas garis tersebut. Artinya, dari A, lintasan tersebut tidak berhenti di B, namun lintasan tersebut diteruskan tanpa berbelok dan tanpa henti. Demikian juga, dari B lintasan tersebut tidak berhenti di A, namun lintasan tersebut diteruskan tanpa berbelok dan tanpa henti. Untuk menyatakan sifat “tidak berhenti” tersebut, digunakan sepasang tanda panah, sehingga garis AB digambarkan sebagai berikut.

Gambar 2
Jadi, perbedaan antara garis dan ruas garis adalah: panjang ruas garis berhingga, sedangkan panjang garis tak berhingga. Garis merupakan perpanjangan tanpa henti suatu ruas garis dalam kedua arah. Dalam menggambarkan garis, digunakan sepasang tanda panah untuk menunjukkan perpanjangan tanpa henti tersebut.
Menentukan garis
Misalkan kita akan menggambarkan suatu garis dalam sistem koordinat Kartesius. Misalkan terdapat titik P(3,4) dan tiga orang, yaitu Anto, Budi, dan Candra diminta untuk menggambarkan garis yang melewati P. Berikut ini adalah garis yang mereka gambarkan.

Gambar 3
Ternyata, dengan perintah yang sama, mereka memberikan jawaban yang berbeda-beda dan semuanya jawaban tersebut benar; yang diminta adalah garis yang melewati P(3,4). Jawaban terhadap perintah tersebut tidak tunggal. Ternyata, hanya dengan menentukan titik yang harus dilalui, tidak diperoleh jawaban yang tunggal.
Sekarang, ketiga orang tersebut diminta untuk membuat garis yang membentuk sudut 450 terhadap sumbu x positif. Berikut adalah jawaban mereka.

Gambar 4
Ternyata, dengan perintah yang sama, mereka masih memberikan jawaban yang berbeda-beda dan semuanya jawaban tersebut benar; yang diminta adalah garis yang membentuk sudut 450 terhadap sumbu x positif. Jawaban terhadap perintah tersebut tidak tunggal. Ternyata, hanya dengan menentukan kemiringan garis, tidak diperoleh jawaban yang tunggal. Jika demikian, apa saja yang harus diketahui mengenai garis tersebut, agar hanya terdapat satu jawaban yang unik/tunggal? Ada beberapa cara menentukan (= membuat jadi tentu) suatu garis.
- Suatu garis dapat ditentukan dengan kemiringan (gradient) dan koordinat titik potong dengan sumbu y.
Garis yang kemiringannya m dan berpotongan dengan sumbu y di (0,c) adalah y = mx + c. Jika m > 0, garis menanjak dari kiri ke kanan. Jika m = 0, garis akan sejajar dengan sumbu x. Jika m < 0 garis menurun dari kiri ke kanan.
Contoh 1:
Persamaan garis dengan gradien 2 yang berpotongan dengan sumbu y di (0,4) adalah y = 2x + 4. Gambar garis tersebut adalah sebagai berikut. (Mengenai cara menggambar garis yang persamaannya diketahui dapat dipelajari di tautan yang tersedia di bagian akhir tulisan ini.)

Gambar 5
Perhatikan pada gambar di atas, bahwa garis menanjak dari kiri ke kanan. Ini adalah karena gradien garis tersebut positif.
Contoh 2:
Persamaan garis dengan gradien -1 yang berpotongan dengan sumbu y di (0,1) adalah y = –x + 1
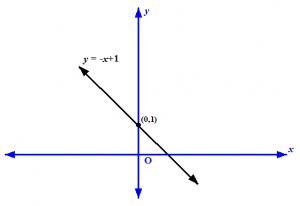
Gambar 6
Perhatikan pada gambar di atas, bahwa garis menurun dari kiri ke kanan. Ini adalah karena gradien garis tersebut negatif.
Contoh 3:
Persamaan garis dengan gradien 0 dan berpotongan dengan sumbu y di (0,-3) adalah y = -3.
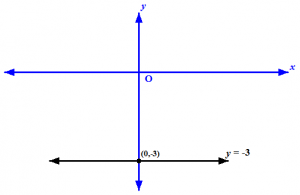
Gambar 7
- Suatu garis dapat ditentukan apabila diketahui dua buah titik yang dilaluinya.
Persamaan garis yang melalui titik A(x1,y1) dan B(x2,y2) dapat dinyatakan sebagai:
![]()
Contoh 4.1.:
Persamaan garis yang melalui A(-1,3) dan B(4,-5) adalah:
![]()

Gambar 8.1.
Khususnya, apabila diketahui koordinat-koordinat titik-titik potong garis dengan sumbu x dan sumbu y, persamaan garis dapat ditentukan dengan:
![]()
Garis tersebut melalui (a,0) dan (0,b).
Contoh 4.2.:
Misalkan suatu garis memotong sumbu x di (4,0) dan memotong sumbu y di (0,-3). Persamaan garis itu dapat ditentukan dengan
![]()

Gambar 8.2.
Apabila diketahui titik-titik dengan koordinat (x1,y1) dan (x2,y2), gradien garis yang melalui kedua titik tersebut dapat dihitung dengan rumus sebagai berikut.
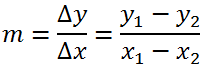
Contoh 4.3.:
Gradien garis yang melalui titik-titik yang berkoordinat (-3,1) dan (2,4) adalah
![]()
(Baca juga: cara cepat menentukan persamaan garis)
- Suatu garis dapat ditentukan apabila diketahui kemiringan dan sebuah titik yang dilaluinya.
Persamaan garis yang bergradien m dan melalui titik berkoordinat (a,b) adalah y – b = m(x – a).
Contoh 5
Persamaan garis yang bergradien ¾ dan melalui (2,5) adalah
![]()
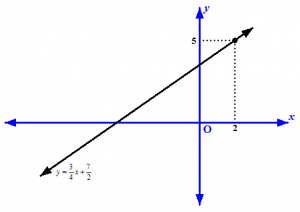
Gambar 9
Berikut ini adalah tautan-tautan yang berkenaan dengan garis atau persamaan garis:
- Cara menggambar garis yang persamaannya diketahui dan latihan soal menggambar garis
- Bentuk lain persamaan garis
- Menentukan koordinat titik potong dua garis
- Latihan soal “Persamaan Garis”: (tautan belum tersedia)
- Cara cepat menentukan persamaan garis
Tagging: gradien, kemiringan, persamaan garis, ruas garis




terima kasih materinya.. membantu