MENENTUKAN KOORDINAT TITIK POTONG DUA GARIS
(English version of this article is available at edsmathscholar.com, click here)
Jika terdapat dua buah garis sebidang yang tidak sejajar maka kedua garis tersebut akan berpotongan. Jika kedua garis itu ditempatkan pada sistem koordinat Kartesius, kita dapat menentukan koordinat titik potong kedua garis tersebut.
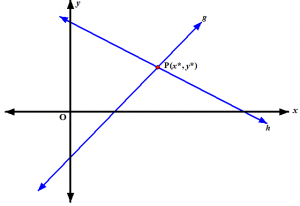
Misalkan diketahui garis g dengan persamaan A1x + B1y + C1 = 0 dan garis h yang tidak sejajar g, dengan persamaan A2x + B2y + C2 = 0. Misalkan kedua garis itu berpotongan di P(x*,y*). (Lihat gambar di bawah.)

Gambar 1
Karena P terletak di kedua garis, tentunya A1x* + B1y* + C1 = 0 dan A2x* + B2y* + C2 = 0. Karena g tidak sejajar h, A1B2 – A2B1 ≠ 0 dan akibatnya nilai x* dan y* dapat ditentukan dengan aneka ragam cara penyelesaian sistem persamaan dengan dua anu (misalnya dengan teknik eliminasi, substitusi, dan lain-lain.) Semua teknik itu akan menghasilkan:
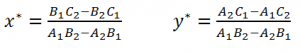
Contoh 1:
Diketahui garis-garis dengan persamaan y = x + 4 dan y = 2x + 1. Tentukan koordinat titik potong kedua garis itu dan gambarkan situasi ini dalam sistem koordinat Kartesius.
Jawab:
Dengan cara substitusi, substitusikan y = x + 4 ke y = 2x + 1, diperoleh persamaan 2x + 1 = x + 4. Dari persamaan ini diperoleh x = 3. Substitusikan x = 3 ini ke y = x + 4 atau y = 2x + 1, diperoleh y = 7. Jadi, koordinat titik potong kedua garis itu adalah (3,7).
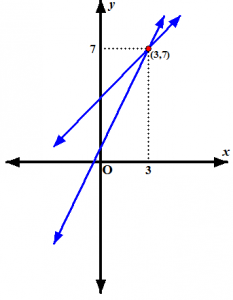
Gambar 2
Contoh 2:
Diketahui garis g dengan persamaan 2x + 3y + 1 = 0 dan garis h dengan persamaan 5x – 3y – 8 = 0. Tentukan koordinat titik potong kedua garis tersebut dan gambarkan situasi ini dalam sistem koordinat Kartesius.
Jawab:
Misalkan kita akan menyelesaikan ini dengan teknik eliminasi.
g ≡ 2x + 3y + 1 = 0 ……………………………… (1)
h ≡ 5x – 3y – 8 = 0 ……………………………… (2)
Untuk menentukan x, eliminasikan y dengan menjumlahkan persamaan (1) dengan (2).
2x + 3y + 1 = 0
5x – 3y – 8 = 0 +
7x – 7 = 0
⇔ x = 1
Untuk menentukan y, eliminasikan x dengan cara mengalikan (1) dengan 5 dan mengalikan (2) dengan (-2), dan kemudian menjumlahkan persamaan-persamaan yang terbentuk.
5.(1) ……………………… 10x + 15y + 5 = 0
-2.(2) …………………….. –10x + 6y + 16 = 0 +
21y + 21 = 0
y = -1
Jadi, diperoleh koordinat titik potong kedua garis tersebut (1,-1).
Dengan rumus x* dan y* yang sudah diuraikan di atas, soal ini dapat pula diselesaikan sebagai berikut.
Dari 2x + 3y + 1 = 0, diperoleh A1 = 2, B1 = 3, C1 = 1.
Dari 5x – 3y – 8 = 0, diperoleh A2 = 5, B2 = -3, C2 = -8.
Substitusikan nilai-nilai tersebut ke dalam rumus x* dan y*, diperoleh:

Jadi, diperoleh koordinat titik potong kedua garis tersebut (1,-1).

Gambar 3
Tentunya masih ada cara-cara lain untuk mencari koordinat titik potong dua garis yang diketahui persamaannya. Pada intinya, mencari koordinat titik potong antara dua garis ini dilakukan dengan mencari solusi/jawab dari sistem persamaan linier yang bersesuaian dengan persamaan-persamaan garis yang diketahui.
Berikut ini adalah tautan-tautan yang berhubungan dengan posting ini.
- Teknik penyelesaian sistem persamaan linier
- Latihan Soal Persamaan Garis (1)
- Menentukan koordinat titik potong dua garis dengan cara analitik




Kak, kan 7x-7=0 tapi kok x=1? saya kurang paham kak?
7x – 7 = 0
7x = 7
x = 1
Kak, kan 7x-7=0 tapi kok x=1? Caranya gimana?
Kak, kan dari 2 persamaan ketemu 1 koordinat kok bisa ada 2 garis, gimana caranya saya kurang paham kak?
Kan memang sejak awalnya juga ada dua garis. Garis yang satu persamaannya 2x+3y+1 = 0 dan yang satunya lagi 5x-3y-8 = 0. Hehehe.
Cara menentukan garis poyong nya tu apa terserah kita ya kak?
poyong itu apa?