BILANGAN BERPANGKAT DAN FUNGSI EKSPONENSIAL

Agustus 6th, 2016

Pangkat nol

a0 = 1 ; a ∊ ℝ, a ≠ 0 [00 tidak terdefinisi]

 

Pangkat bilangan asli

a1 = a ; \textit{a} \in \mathbb{R}

an = a1.a2.a3. … an dengan a1 = a2 = a3 = … = an = a, n \in \mathbb{N}

Contoh:

53 = 5.5.5 = 125

0,14 = 0,1 . 0,1 . 0,1 . 0,1 = 0,0001

 

Pangkat bilangan bulat negatif

a^{-n}=\frac{1}{a^n}  ; n \in \mathbb{N}, \: a \in \mathbb{R}, a ≠ 0

Contoh:

7^{-1}=\frac{1}{7^1}=\frac{1}{7}

3^{-4}=\frac{1}{3^4}=\frac{1}{3.3.3.3}=\frac{1}{81}

 

Pangkat bilangan rasional

a^{\frac{1}{2}}=\sqrt{a}  ; a \in \mathbb{R}, a ≥ 0   [akar kuadrat]

Contoh:

16^{\frac{1}{2}}=\sqrt{16}=4

 

a^{\frac{1}{2n}}=\sqrt[2n]{a}  ; n \in \mathbb{N}, \: a \in \mathbb{R}, a ≥ 0   [akar pangkat bilangan genap positif]

Contoh:

10000^{\frac{1}{4}}=\sqrt[4]{10000}

 

a^{\frac{1}{2n+1}}=\sqrt[2n+1]{a}  ; n \in \mathbb{N}, \: a \in \mathbb{R}  [akar pangkat bilangan ganjil positif]

Contoh:

125^{\frac{1}{3}}=\sqrt[3]{125}=5

(-32)^{\frac{1}{5}}=\sqrt[5]{-32}=-2

(-128)^{\frac{1}{7}}=\sqrt[7]{-128}=-2

 

a^{\frac{m}{2n}}=(a^{\frac{1}{2n}})^m=(a^m)^{\frac{1}{2n}}  ; m, n \in \mathbb{N}, \: a \in \mathbb{R}, a ≥ 0

Contoh:

81^{\frac{3}{4}}=(81^{\frac{1}{4}})^3=(\sqrt[4]{81})^3=3^3=27

4^{\frac{5}{2}}=(4^5)^{\frac{1}{2}}=1024^{\frac{1}{2}}=\sqrt{1024}=32

 

a^{\frac{m}{2n+1}}=(a^{\frac{1}{2n+1}})^m=(a^m)^{\frac{1}{2n+1}}   ; m, n \in \mathbb{N}, a \in \mathbb{R}

Contoh:

(-125)^{\frac{5}{3}}={\left[ (-125)^{\frac{1}{3}} \right]}^5=(\sqrt[3]{-125})^5=(-5)^5=-3125

0,00001^{\frac{7}{5}}=(0,00001^{\frac{1}{5}})^7=(\sqrt[5]{0,00001})^7=0,1^7=0,0000001

8^{\frac{2}{3}}=(8^2)^{\frac{1}{3}}=64^{\frac{1}{3}}=\sqrt[3]{64}=4

 

a^{\frac{-m}{2n}}=\frac{1}{a^{\frac{m}{2n}}}   ; m, n \in \mathbb{N}, \: a \in \mathbb{R}, a > 0

Contoh:

81^{\frac{-3}{4}}=\frac{1}{81^{\frac{3}{4}}}=\frac{1}{(81^{\frac{1}{4}})^3}=\frac{1}{(\sqrt[4]{81})^3}=\frac{1}{3^3}=\frac{1}{27}

4^{\frac{-5}{2}}=\frac{1}{4^{\frac{5}{2}}}=\frac{1}{(4^5)^{\frac{1}{2}}}=\frac{1}{1024^{\frac{1}{2}}}=\frac{1}{\sqrt{1024}}=\frac{1}{32}

 

a^{\frac{-m}{2n+1}}=\frac{1}{a^{\frac{m}{2n+1}}}  ; m, n \in \mathbb{N}, a \: \in \mathbb{R}, a ≠ 0

Contoh:

(-125)^{\frac{-5}{3}}=\frac{1}{(-125)^{\frac{5}{3}}}=\frac{1}{{\left[ (-125)^{\frac{1}{3}}\right]}^5}=\frac{1}{(\sqrt[3]{-125})^5}=\frac{1}{(-5)^5}=\frac{1}{-3125}

8^{\frac{-2}{3}}=\frac{1}{8^{\frac{2}{3}}}=\frac{1}{(8^2)^{\frac{1}{3}}}=\frac{1}{64^{\frac{1}{3}}}=\frac{1}{\sqrt[3]{64}}=\frac{1}{4}

 

Bagaimana dengan pangkat-pangkat yang merupakan bilangan irasional? Misalnya, bagaimana menghitung 5^{\sqrt{3}}? Tentu ini menghasilkan bilangan irasional juga, yang representasi desimalnya hanya merupakan pendekatan dengan galat (error) tertentu. Ini akan dibahas di bagian lain dalam website ini.

 

Rumus-rumus mengenai pemangkatan

(perhatikan syarat-syarat keberlakuan rumus R1 sampai dengan R5 berikut di bagian setelah R5.)

R1: a^m \cdot a^n=a^{m+n}

R2: \frac{a^m}{a^n}=a^{m-n}

R3: (a^m)^n=(a^n)^m=a^{mn}

R4: (a \cdot b)^n=a^n \cdot b^n

R5: (\frac{a}{b})^n=\frac{a^n}{b^n}

Keterangan penggunaan rumus dan syarat keberlakuan rumus-rumus tersebut:

  1. a, b, m, n \in \mathbb{R}
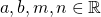
  2. Pada R2 a ≠ 0 dan pada R5 b ≠ 0
  3. R1 sampai dengan R5 berlaku dengan syarat pemangkatan atau operasi aljabar lainnya terdefinisi. Sebagai contoh, dalam penggunaan R1 kita tak boleh menyatakan 05.0-2 = 03 karena 0-2 tidak terdefinisi. Contoh lain, misalnya dalam penggunaan R1, kita tak boleh menyatakan 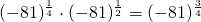(-81)^{\frac{1}{4}} \cdot (-81)^{\frac{1}{2}}=(-81)^{\frac{3}{4}} karena (-81)^{\frac{1}{4}} tidak terdefinisi, demikian halnya juga dengan (-81)^{\frac{1}{2}} dan (-81)^{\frac{3}{4}}.

 

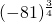Fungsi eksponensial

Misalkan a ∊ ℝ dengan a > 0 dan a ≠ 1 . Fungsi eksponensial adalah suatu fungsi f dari ℝ ke ℝ, dengan f(x) = ax untuk setiap x ∊ ℝ. Jika a > 1 f monoton naik sedangkan jika 0 < a < 1 f monoton turun. a dinamakan basis fungsi eksponensial tersebut.

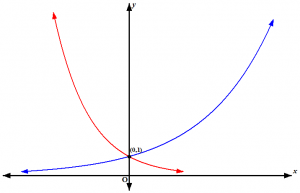
Eksponen_01

Pada gambar di atas, kurva biru adalah tipikal bentuk kurva y = ax apabila a > 1 sedangkan yang berwarna merah adalah tipikal bentuk kurva y = ax apabila 0 < a < 1. Setiap grafik y = ax berpotongan dengan sumbu y di (0,1). Ini merupakan akibat dari a0 =1 untuk setiap a ∊ ℝ dengan a ≠ 0. Selanjutnya, sumbu x merupakan asimtot datar kurva y = ax; walaupun kurva semakin mendekati sumbu x, namun kurva tersebut tidak memotong sumbu x.

 

Salah satu fungsi eksponensial yang penting adalah fungsi eksponensial dengan e (bilangan Euler) sebagai basisnya. Fungsi ini dinamakan fungsi eksponensial alami, yaitu suatu fungsi f dari ℝ ke ℝ dengan f(x) = ex untuk setiap x ∊ ℝ. Fungsi ini banyak sekali penerapannya di berbagai bidang, baik ilmu alam maupun ilmu sosial.

 

Tagging: ,

Most visitors also read :



Satu tanggapan untuk “BILANGAN BERPANGKAT DAN FUNGSI EKSPONENSIAL”

  1. Wulan Rizqya Rindyliana berkata:
    November 14, 2020 pukul 13:26

    Nama : Wulan Rizqya Rindyliana
    Npm : 5203009

    Balas

Tinggalkan Balasan

Alamat email Anda tidak akan dipublikasikan.