Tidak banyak orang yang bisa menjelaskan apa artinya tiga perempat (3/4). Kata-kata seperti seperempat, tiga perempat memang sering terdengar dalam keseharian kita. Tapi kalau kita pikirkan lebih lanjut, bagaimana kita menerangkan apa itu tiga perempat? Seberapa banyak tiga perempat tersebut? Lebih sedikit lagi orang yang bisa menerangkan apa artinya lima belas perdua puluh tiga (15/23). Seberapa banyak lima belas perdua puluh tiga itu? Barangkali yang bisa menjelaskan itu hanya sarjana-sarjana matematika.
Tulisan saya kali ini membahas bilangan-bilangan rasional, di mana nanti kita ketahui bahwa ¾ merupakan suatu bilangan rasional. Konstruksi bilangan rasional ini sebenarnya tidak sesederhana yang diuraikan dalam tulisan ini, banyak mathematical details yang tidak ditampilkan di sini. Dalam tulisan ini saya hanya berusaha memperkenalkan bilangan-bilangan rasional untuk khalayak umum sehingga pembahasannya dibuat sesederhana mungkin tanpa mengurangi nilai kebenaran pernyataan-pernyataan mengenai bilangan rasional.
Di tulisan yang lalu, saya telah memperkenalkan bilangan asli dan bilangan bulat. Dapat dibaca pada tulisan tersebut bagaimana himpunan semua bilangan asli ℕ berkembang menjadi ℤ, himpunan semua bilangan bulat; dari semula kita hanya memiliki {1, 2, 3, 4, 5, …} hingga kita memiliki {…, -4, -3, -2, -1, 0, 1, 2, 3, …}. Apakah dengan memiliki ℤ itu sudah cukup/memadai? Mari kita tinjau beberapa persamaan berikut. Adakah bilangan bulat yang apabila dikalikan 5 menghasilkan 10? [Adakah x ∊ ℤ yang memenuhi 5x = 10?] Ada, yaitu x = 2. Adakah bilangan bulat yang dikalikan -3 menghasilan 12? [Adakah x ∊ ℤ yang memenuhi -3x = 12?] Ada, yaitu x = -4. Sekarang, adakah bilangan bulat yang dikalikan 4 menghasilkan 1? [Adakah x ∊ ℤ yang memenuhi 4x = 3?] Setiap bilangan bulat apabila dikalikan 4 tidak mungkin menghasilkan 3! Ini menunjukkan bahwa ternyata ℤ masih “menyisakan masalah.” Tidak semua persamaan dalam x yang berbentuk ax = b dapat memiliki penyelesaian dalam ℤ! Karena itulah kita “perlu” mengembangkan lagi himpunan bilangan lain yang dapat menyelesaikan lebih banyak persamaan. Dalam rangka itu, kita selanjutnya memiliki ℚ, yaitu himpunan semua bilangan rasional.
Sekarang bagaimana mendefinisikan ℚ? . Secara mudahnya, dapat dijelaskan sebagai berikut. Anggota-anggota ℚ merupakan pasangan-pasangan bilangan bilangan bulatm dan n dalam bentuk atau m/n (yang dinamakan pecahan/fraction). Dalam pecahan m/n, m dinamakan pembilang (numerator) dan n dinamakan (denominator). Baik m maupun n keduanya harus merupakan bilangan bulat namun n tidak boleh bernilai 0 (n ≠ 0). Beberapa contoh bilangan rasional tersebut adalah . Tentunya terdapat tak berhingga banyaknya bilangan rasional. Secara umum, adalah bilangan rasional yang apabila dikalikan dengan n akan menghasilkan m. Jadi, misalnya adalah bilangan rasional yang apabila dikalikan dengan 7 akan menghasilkan 2. Demikian juga adalah bilangan rasional yang apabila dikalikan dengan -17 akan menghasilkan 9, dan seterusnya.
Setiap bilangan bulat merupakan bilangan rasional. Secara matematis, ℤ ⊆ ℚ. Kehadiran ℚ “menutupi” kekurangan ℤ. Persamaan 4x = 3 tidak memiliki jawab apabila x ∊ ℤ. Namun apabila x ∊ ℚ, persamaan tersebut memiliki penyelesaian yaitu x = ¾. Tiga perempat merupakan bilangan rasional yang merupakan jawab dari persamaan 4x = 3. Secara umum, bilangan rasional m/n merupakan jawab dari persamaan nx = m apabila m, n∊ℤ, n ≠ 0 dan x∊ℚ.
Berikut adalah beberapa link yang berkaitan dengan bilangan rasional:
Representasi desimal bilangan rasional: (link belum tersedia)
Bilangan rasional sebagai nilai pendekatan bilangan irasional: (link belum tersedia)
APAKAH TIGA PEREMPAT ITU?
Tidak banyak orang yang bisa menjelaskan apa artinya tiga perempat (3/4). Kata-kata seperti seperempat, tiga perempat memang sering terdengar dalam keseharian kita. Tapi kalau kita pikirkan lebih lanjut, bagaimana kita menerangkan apa itu tiga perempat? Seberapa banyak tiga perempat tersebut? Lebih sedikit lagi orang yang bisa menerangkan apa artinya lima belas perdua puluh tiga (15/23). Seberapa banyak lima belas perdua puluh tiga itu? Barangkali yang bisa menjelaskan itu hanya sarjana-sarjana matematika.
Tulisan saya kali ini membahas bilangan-bilangan rasional, di mana nanti kita ketahui bahwa ¾ merupakan suatu bilangan rasional. Konstruksi bilangan rasional ini sebenarnya tidak sesederhana yang diuraikan dalam tulisan ini, banyak mathematical details yang tidak ditampilkan di sini. Dalam tulisan ini saya hanya berusaha memperkenalkan bilangan-bilangan rasional untuk khalayak umum sehingga pembahasannya dibuat sesederhana mungkin tanpa mengurangi nilai kebenaran pernyataan-pernyataan mengenai bilangan rasional.
Di tulisan yang lalu, saya telah memperkenalkan bilangan asli dan bilangan bulat. Dapat dibaca pada tulisan tersebut bagaimana himpunan semua bilangan asli ℕ berkembang menjadi ℤ, himpunan semua bilangan bulat; dari semula kita hanya memiliki {1, 2, 3, 4, 5, …} hingga kita memiliki {…, -4, -3, -2, -1, 0, 1, 2, 3, …}. Apakah dengan memiliki ℤ itu sudah cukup/memadai? Mari kita tinjau beberapa persamaan berikut. Adakah bilangan bulat yang apabila dikalikan 5 menghasilkan 10? [Adakah x ∊ ℤ yang memenuhi 5x = 10?] Ada, yaitu x = 2. Adakah bilangan bulat yang dikalikan -3 menghasilan 12? [Adakah x ∊ ℤ yang memenuhi -3x = 12?] Ada, yaitu x = -4. Sekarang, adakah bilangan bulat yang dikalikan 4 menghasilkan 1? [Adakah x ∊ ℤ yang memenuhi 4x = 3?] Setiap bilangan bulat apabila dikalikan 4 tidak mungkin menghasilkan 3! Ini menunjukkan bahwa ternyata ℤ masih “menyisakan masalah.” Tidak semua persamaan dalam x yang berbentuk ax = b dapat memiliki penyelesaian dalam ℤ! Karena itulah kita “perlu” mengembangkan lagi himpunan bilangan lain yang dapat menyelesaikan lebih banyak persamaan. Dalam rangka itu, kita selanjutnya memiliki ℚ, yaitu himpunan semua bilangan rasional.
Sekarang bagaimana mendefinisikan ℚ?
. Secara mudahnya, dapat dijelaskan sebagai berikut. Anggota-anggota ℚ merupakan pasangan-pasangan bilangan bilangan bulat m dan n dalam bentuk 
atau m/n (yang dinamakan pecahan/fraction). Dalam pecahan m/n, m dinamakan pembilang (numerator) dan n dinamakan (denominator). Baik m maupun n keduanya harus merupakan bilangan bulat namun n tidak boleh bernilai 0 (n ≠ 0). Beberapa contoh bilangan rasional tersebut adalah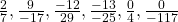 
. Tentunya terdapat tak berhingga banyaknya bilangan rasional. Secara umum, 
adalah bilangan rasional yang apabila dikalikan dengan n akan menghasilkan m. Jadi, misalnya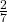 
adalah bilangan rasional yang apabila dikalikan dengan 7 akan menghasilkan 2. Demikian juga 
adalah bilangan rasional yang apabila dikalikan dengan -17 akan menghasilkan 9, dan seterusnya.
Setiap bilangan bulat merupakan bilangan rasional. Secara matematis, ℤ ⊆ ℚ. Kehadiran ℚ “menutupi” kekurangan ℤ. Persamaan 4x = 3 tidak memiliki jawab apabila x ∊ ℤ. Namun apabila x ∊ ℚ, persamaan tersebut memiliki penyelesaian yaitu x = ¾. Tiga perempat merupakan bilangan rasional yang merupakan jawab dari persamaan 4x = 3. Secara umum, bilangan rasional m/n merupakan jawab dari persamaan nx = m apabila m, n ∊ ℤ, n ≠ 0 dan x ∊ ℚ.
Berikut adalah beberapa link yang berkaitan dengan bilangan rasional:
Bagikan ini:
Most visitors also read :
BERKENALAN DENGAN NILAI DAN VEKTOR EIGEN
DEKOMPOSISI NILAI SINGULAR (SINGULAR VALUE DECOMPOSITION)
MATRIKS AKAR KUADRAT
SOAL DAN PEMBAHASAN ANALISIS KOMPONEN UTAMA