PERSAMAAN GARIS BAGI SUDUT ANTARA DUA GARIS

September 18th, 2016

garis_bagi_sudut_dua_garis_03

Pada posting kali ini saya akan menguraikan bagaimana cara menentukan persamaan garis-bagi sudut antara dua garis yang persamaannya diketahui. Sebagai contoh, misalkan diketahui garis h dengan persamaan y = \frac{x}{2} dan garis g dengan persamaan y=\frac{7}{2} x. Pada Gambar 1, garis g berwarna hijau dan garis h berwarna hitam.

 

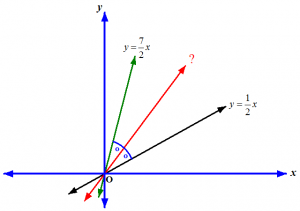
garis_bagi_sudut_dua_garis_01

Gambar 1

 

Garis merah pada gambar di atas membagi dua sama besar sudut yang dibentuk oleh garis merah dan hijau. Inilah yang dimaksud dengan garis-bagi sudut antara dua garis. Bagaimana persamaan garis-bagi ini? Inilah yang akan dijawab pada posting kali ini.

 

Kita turunkan dulu rumusnya …..

 

Diketahui:

  1. garis g dengan persamaan A1x + B1y + C1 = 0,
  2. garis h dengan persamaan A2x + B2y + C2 = 0,
  3. garis k yang merupakan garis-bagi sudut antara g dan h

Ditanyakan: persamaan garis k

Jawab:

Misalkan P0(x0,y0) adalah sembarang titik yang terletak di k. Misalkan A terletak di garis g sedemikian hingga \overline{AP_0} \: \bot \: g dan B di garis h sedemikian hingga \overline{BP_0} \: \bot \: h. Dengan kata lain \vert \overline{AP_0} \vert = jarak antara P0 terhadap g dan \vert \overline{BP_0} \vert = jarak antara P0 terhadap h. (Lihat Gambar 2.)

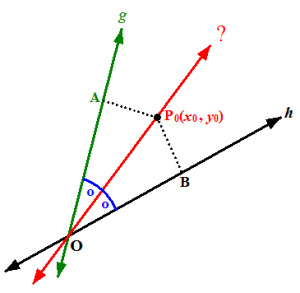
garis_bagi_sudut_dua_garis_02

Gambar 2

 

Pada Gambar 2, O merupakan titik potong antara g dan h. Perhatikan bahwa OP0 pada ΔOAP0 bersekutu dengan OP0 pada ΔOBP0 (sehingga sama panjang) dan ∠AOP0 = ∠BOP0 sehingga ΔOAP0 ≌ ΔOBP0. Karena itu \vert \overline{AP_0} \vert = \vert \overline{BP_0} \vert. Dengan mempergunakan rumus jarak antara titik ke garis, diperoleh:

\frac{\vert A_1 x_0 + B_1 y_0 + C_1 \vert}{\sqrt{{A_1}^2 + {B_1}^2}} = \frac{\vert A_2 x_0 + B_2 y_0 + C_2 \vert}{\sqrt{{A_2}^2 + {B_2}^2}}

\frac{A_1 x_0 + B_1 y_0 + C_1}{\sqrt{{A_1}^2 + {B_1}^2}} = \pm \frac{A_2 x_0 + B_2 y_0 + C_2}{\sqrt{{A_2}^2 + {B_2}^2}}

Karena P0(x0,y0) adalah sembarang titik di k, kesamaan terakhir di atas berlaku untuk semua titik di k sehingga persamaan garis k dapat dinyatakan sebagai:

\frac{A_1 x + B_1 y + C_1}{\sqrt{{A_1}^2 + {B_1}^2}} = \pm \frac{A_2 x + B_2 y + C_2}{\sqrt{{A_2}^2 + {B_2}^2}} ……………………………………………………………………………… (*)

 

Perhatikan bahwa dari (*) tampak bahwa sebenarnya terdapat dua buah garis-bagi yang mungkin.

Selalu terdapat dua buah garis-bagi untuk setiap pasang garis yang diminta persamaan garis-baginya.

Garis bagi lainnya tersebut pada Gambar 3 diwarnai kuning.

 

garis_bagi_sudut_dua_garis_03

Gambar 3

 

Tadi dikatakan bahwa terdapat dua buah garis-bagi untuk setiap pasang garis yang diminta persamaan garis-baginya. Bagaimana hubungan di antara kedua garis-bagi tersebut? Dapat dibuktikan bahwa:

kedua garis-bagi tersebut saling tegaklurus satu sama lain.

 

Sekarang kita siap menyelesaikan soal yang ditanyakan di bagian awal posting ini.

 

Diketahui:

  1. garis g dengan persamaan y=\frac{7}{2} x
  2. garis h dengan persamaan y = \frac{x}{2}

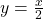
Ditanyakan: persamaan garis-bagi antara garis g dan h tersebut.

Jawab:

Perhatikan bahwa garis g dan h dapat dinyatakan dalam bentuk Ax + By + C = 0 sebagai berikut:

g ≡ 7x – 2y = 0

h ≡ x – 2y = 0

Substitusikan A1 = 7, B1 = -2, C1 = 0, A2 = 1, B2 = -2, dan C2 = 0 ke dalam rumus (*), diperoleh:

\frac{7x-2y}{\sqrt{7^2+(-2)^2}} = \pm \frac{x-2y}{\sqrt{1^2+(-2)^2}}

Terdapat dua garis-bagi, yaitu sebagai berikut.

 

Garis-bagi pertama: (Lihat Gambar 4)

\frac{7x-2y}{\sqrt{7^2+(-2)^2}} = \frac{x-2y}{\sqrt{1^2+(-2)^2}}

\Leftrightarrow y = \frac{3 - \sqrt{265}}{16} x

 

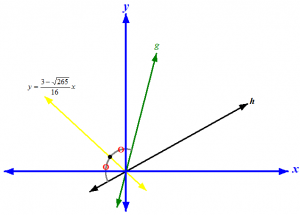
garis_bagi_sudut_dua_garis_04

Gambar 4

 

Garis-bagi kedua: (Lihat Gambar 5)

\frac{7x-2y}{\sqrt{7^2+(-2)^2}} = - \frac{x-2y}{\sqrt{1^2+(-2)^2}}

\Leftrightarrow y = \frac{3 + \sqrt{265}}{16} x

 

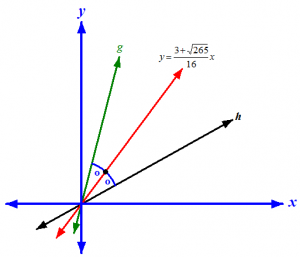
garis_bagi_sudut_dua_garis_05

Gambar 5

 

 

Tagging:

Most visitors also read :



Satu tanggapan untuk “PERSAMAAN GARIS BAGI SUDUT ANTARA DUA GARIS”

  1. Fatma Erlianti berkata:
    April 25, 2017 pukul 09:52

    Terimakasih sngat membantu

    Balas

Tinggalkan Balasan

Alamat email Anda tidak akan dipublikasikan.