Di tulisan saya yang lalu (berjudul “Apakah Tiga Perempat Itu?”), saya telah memperkenalkan bilangan rasional (rational numbers). Kali ini saya akan memperkenalkan bilangan-bilangan irasional (irrational numbers). Dengan memperhatikan awalan/prefix bahasa Inggris irr– (yang berarti penyangkalan) dengan mudah kita dapat mengetahui bahwa bilangan irasional berarti bilangan yang tidak rasional. Jadi, bilangan tersebut tidak mungkin dinyatakan dalam bentuk a/b dengan a, b ∊ ℤ dan b ≠ 0.
Mari kita lihat sebuah contoh. Berapakah x ∊ ℚ yang memenuhi x2 = 2? Karena x yang “diminta” ini harus merupakan bilangan rasional, soal ini meminta kita mencari a dan b (b ≠ 0) yang keduanya merupakan bilangan bulat, sedemikian hingga:
Kita bisa saja mencoba-coba, misalnya:
atau atau atau
dan seterusnya, namun tidak akan pernah bisa berhasil mendapatkan hasil akhir 2 sebagaimana yang diinginkan. Ini menunjukkan bahwa x yang memenuhi persamaan x2 = 2 tentunya tidak rasional atau irasional. Selanjutnya, nilai x yang memenuhi persamaan tersebut “dilambangkan” dengan .
Mari kita lihat contoh lainnya. Berapakah y ∊ ℚ yang memenuhi yang memenuhi y3 = 10? Dengan kata lain, kita mencari nilai p, q ∊ ℤ, q ≠ 0 sedemikian hingga . Kita bisa saja mencoba-coba, misalnya
atau atau
dan seterusnya, namun … kita tidak akan pernah bisa berhasil mendapatkan hasil akhir 10. Ini menunjukkan bahwa y yang memenuhi y3 = 10 tidak mungkin rasional. Dengan kata lain, y tersebut irasional. Selanjutnya, nilai y yang memenuhi persamaan tersebut “dilambangkan” dengan .
Bukan hanya itu, nilai t yang memenuhi 10t = 3 juga tidak mungkin rasional. Nilai t yang memenuhi persamaan tersebut selanjutnya “dilambangkan” dengan log 3 ∉ ℚ. Demikian juga nilai u yang memenuhi 2u = 5 juga tidak mungkin rasional. Nilai u yang memenuhi persamaan tersebut selanjutnya “dilambangkan” dengan 2log 5 ∉ ℚ.
Masih banyak sekali (bahkan tak berhingga banyaknya) bilangan irasional itu, termasuk bilangan π, bilangan e (bilangan Euler), sin 100, , dan sebagainya. Bahkan bilangan irasional lebih banyak daripada bilangan rasional. Jika semua bilangan irasional tersebut kita “kumpulkan” di suatu himpunan (anggaplah nama himpunan tersebut adalah Irr) dan kemudian Irr tersebut kita “gabungkan” dengan ℚ, maka himpunan hasil gabungan keduanya adalah ℝ, yaitu himpunan seluruh bilangan nyata (real numbers). Jadi, secara matematis dapat kita nyatakan ℝ = ℚ∪ Irr.
“Tumbuh kembang” aneka jenis bilangan yang sudah pernah saya tulis di website ini dapat diilustrasikan sebagai berikut.
Pada ℕ dan ℤ, tampak bahwa “jarak” antara bilangan yang satu dengan yang lain “berjauhan” satu sama lain. Artinya, tidak ada bilangan asli atau bilangan bulat yang terletak di antara dua bilangan asli atau bilangan bulat yang berturutan. Sebagai contoh, tidak ada bilangan asli yang lebih besar dari 5 tapi lebih kecil dari 6. Juga, tidak ada bilangan bulat yang lebih besar dari -5 tapi lebih kecil dari -4, dan seterusnya.
Lain halnya dengan ℚ. Pada gambar di atas tampak bahwa bilangan-bilangan rasional terletak sangat berdekatan satu sama lain, sangat rapat. Di antara setiap dua bilangan rasional yang nilainya berbeda, pasti terdapat bilangan rasional lainnya yang terletak di antara kedua bilangan semula. Contoh, di antara ½ dan ¾ (keduanya merupakan bilangan rasional) terdapat bilangan rasional lain, misalnya 5/8. Perhatikan bahwa ½ < 5/8 < ¾. Di antara ½ dan 5/8 itu sendiri pun masih ada bilangan rasional lain yang letaknya di antara keduanya, misalnya adalah 9/16. Perhatikan bahwa ½ < 9/16 < 5/8. Demikian seterusnya.
Namun, walaupun bilangan-bilangan rasional tersebut sangat rapat satu sama lain, tetap masih meninggalkan “lubang-lubang” atau “celah-celah” (kosong). Di sanalah tempatnya bilangan-bilangan irasional! Jadi, bilangan-bilangan irasional tersebut “menutupi” semua celah yang ada dalam ℚ sehingga semua celah tertutup, dan muncullah suatu garis utuh yang menggambarkan ℝ, himpunan semua bilangan nyata. Itulah sebabnya mengapa ℝ biasa digambarkan dengan suatu garis.
Demikianlah perkenalan kita dengan bilangan-bilangan nyata. Hal-hal lain mengenai ℝ dapat diunduh dari tautan-tautan berikut.
BERKENALAN DENGAN BILANGAN NYATA
Di tulisan saya yang lalu (berjudul “Apakah Tiga Perempat Itu?”), saya telah memperkenalkan bilangan rasional (rational numbers). Kali ini saya akan memperkenalkan bilangan-bilangan irasional (irrational numbers). Dengan memperhatikan awalan/prefix bahasa Inggris irr– (yang berarti penyangkalan) dengan mudah kita dapat mengetahui bahwa bilangan irasional berarti bilangan yang tidak rasional. Jadi, bilangan tersebut tidak mungkin dinyatakan dalam bentuk a/b dengan a, b ∊ ℤ dan b ≠ 0.
Mari kita lihat sebuah contoh. Berapakah x ∊ ℚ yang memenuhi x2 = 2? Karena x yang “diminta” ini harus merupakan bilangan rasional, soal ini meminta kita mencari a dan b (b ≠ 0) yang keduanya merupakan bilangan bulat, sedemikian hingga:
Kita bisa saja mencoba-coba, misalnya:
dan seterusnya, namun tidak akan pernah bisa berhasil mendapatkan hasil akhir 2 sebagaimana yang diinginkan. Ini menunjukkan bahwa x yang memenuhi persamaan x2 = 2 tentunya tidak rasional atau irasional. Selanjutnya, nilai x yang memenuhi persamaan tersebut “dilambangkan” dengan
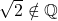 .
.
Mari kita lihat contoh lainnya. Berapakah y ∊ ℚ yang memenuhi yang memenuhi y3 = 10? Dengan kata lain, kita mencari nilai p, q ∊ ℤ, q ≠ 0 sedemikian hingga . Kita bisa saja mencoba-coba, misalnya
. Kita bisa saja mencoba-coba, misalnya
dan seterusnya, namun … kita tidak akan pernah bisa berhasil mendapatkan hasil akhir 10. Ini menunjukkan bahwa y yang memenuhi y3 = 10 tidak mungkin rasional. Dengan kata lain, y tersebut irasional. Selanjutnya, nilai y yang memenuhi persamaan tersebut “dilambangkan” dengan![Rendered by QuickLaTeX.com \sqrt[3]{10} \notin \mathbb{Q}](http://edscyclopedia.com/wp-content/ql-cache/quicklatex.com-efe0f1aef74ad6f8ff4c77c731b9f492_l3.png) .
.
Bukan hanya itu, nilai t yang memenuhi 10t = 3 juga tidak mungkin rasional. Nilai t yang memenuhi persamaan tersebut selanjutnya “dilambangkan” dengan log 3 ∉ ℚ. Demikian juga nilai u yang memenuhi 2u = 5 juga tidak mungkin rasional. Nilai u yang memenuhi persamaan tersebut selanjutnya “dilambangkan” dengan 2log 5 ∉ ℚ.
Masih banyak sekali (bahkan tak berhingga banyaknya) bilangan irasional itu, termasuk bilangan π, bilangan e (bilangan Euler), sin 100, , dan sebagainya. Bahkan bilangan irasional lebih banyak daripada bilangan rasional. Jika semua bilangan irasional tersebut kita “kumpulkan” di suatu himpunan (anggaplah nama himpunan tersebut adalah Irr) dan kemudian Irr tersebut kita “gabungkan” dengan ℚ, maka himpunan hasil gabungan keduanya adalah ℝ, yaitu himpunan seluruh bilangan nyata (real numbers). Jadi, secara matematis dapat kita nyatakan ℝ = ℚ∪ Irr.
“Tumbuh kembang” aneka jenis bilangan yang sudah pernah saya tulis di website ini dapat diilustrasikan sebagai berikut.
Pada ℕ dan ℤ, tampak bahwa “jarak” antara bilangan yang satu dengan yang lain “berjauhan” satu sama lain. Artinya, tidak ada bilangan asli atau bilangan bulat yang terletak di antara dua bilangan asli atau bilangan bulat yang berturutan. Sebagai contoh, tidak ada bilangan asli yang lebih besar dari 5 tapi lebih kecil dari 6. Juga, tidak ada bilangan bulat yang lebih besar dari -5 tapi lebih kecil dari -4, dan seterusnya.
Lain halnya dengan ℚ. Pada gambar di atas tampak bahwa bilangan-bilangan rasional terletak sangat berdekatan satu sama lain, sangat rapat. Di antara setiap dua bilangan rasional yang nilainya berbeda, pasti terdapat bilangan rasional lainnya yang terletak di antara kedua bilangan semula. Contoh, di antara ½ dan ¾ (keduanya merupakan bilangan rasional) terdapat bilangan rasional lain, misalnya 5/8. Perhatikan bahwa ½ < 5/8 < ¾. Di antara ½ dan 5/8 itu sendiri pun masih ada bilangan rasional lain yang letaknya di antara keduanya, misalnya adalah 9/16. Perhatikan bahwa ½ < 9/16 < 5/8. Demikian seterusnya.
Namun, walaupun bilangan-bilangan rasional tersebut sangat rapat satu sama lain, tetap masih meninggalkan “lubang-lubang” atau “celah-celah” (kosong). Di sanalah tempatnya bilangan-bilangan irasional! Jadi, bilangan-bilangan irasional tersebut “menutupi” semua celah yang ada dalam ℚ sehingga semua celah tertutup, dan muncullah suatu garis utuh yang menggambarkan ℝ, himpunan semua bilangan nyata. Itulah sebabnya mengapa ℝ biasa digambarkan dengan suatu garis.
Demikianlah perkenalan kita dengan bilangan-bilangan nyata. Hal-hal lain mengenai ℝ dapat diunduh dari tautan-tautan berikut.
Bagikan ini:
Most visitors also read :
BERKENALAN DENGAN NILAI DAN VEKTOR EIGEN
DEKOMPOSISI NILAI SINGULAR (SINGULAR VALUE DECOMPOSITION)
MATRIKS AKAR KUADRAT
SOAL DAN PEMBAHASAN ANALISIS KOMPONEN UTAMA