PENERAPAN TURUNAN DALAM OPTIMASI DI BIDANG EKONOMI
Maret 28th, 2017
Post kali ini menyajikan beberapa contoh bagaimana konsep turunan digunakan dalam optimasi di bidang ekonomi atau bisnis.
Contoh 1: (Meminimumkan Biaya Rata-rata)
Dalam produksi suatu barang, biaya totalnya adalah TC = (0,4Q2 + 500Q + 16000) rupiah. Berapakah banyaknya barang yang harus diproduksi agar biaya rata-ratanya (AC) minimum? Berapakah biaya rata-rata ninimum tersebut?
Jawab:
Biaya rata-rata (AC) dapat dinyatakan sebagai:
………………………………………………. (*1)
Untuk meminimumkan AC, bentuk persamaan . Dengan rumus turunan, diperoleh:
Dengan membuat , diperoleh persamaan:
0,4 Q2 – 16000 = 0
Q2 – 40000 = 0
(Q+200)(Q-200) = 0
Q1 = -200 dan Q2 = 200 [Q = -200 atau Q = 200]
Di sini diperoleh dua buah titik stasioner, yaitu Q1 = -200 dan Q2 = 200. Untuk menentukan mana di antara kedua nilai ini yang menghasilkan AC minimum, kita tentukan dulu AC”(Q) = , yaitu turunan dari terhadap Q. Dengan menggunakan rumus-rumus turunan, diperoleh:
Jika Q = -200 maka nilai turunan kedua AC terhadap Q adalah
Karena turunan kedua AC terhadap Q tersebut negatif, nilai Q = -200 menghasilkan nilai maksimum relatif biaya rata-rata.
Jika Q = 200 maka nilai turunan kedua AC terhadap Q adalah:
Karena turunan kedua AC terhadap Q tersebut positif, nilai Q = 200 menghasilkan nilai minimum relatif biaya rata-rata.
Jadi, agar biaya rata-rata minimum, banyaknya barang yang harus diproduksi adalah 200 unit.
Untuk menentukan berapa biaya rata-rata yang minimum tersebut, substitusikan Q = 200 ke dalam (*1), diperoleh:
Jadi, biaya rata-rata minimumnya adalah Rp 660/unit.
Contoh 2 (Memaksimalkan Penerimaan Total)
Diketahui permintaan terhadap suatu produk mengikuti persamaan berikut: P = (2700 – 9Q2) rupiah/unit. Berapakah banyaknya produk yang harus terjual agar penerimaan total (TR, Total Revenue) dari hasil penjualan tersebut maksimum?
Jawab:
Jika Q unit produk terjual maka penerimaan total (TR) yang terjadi adalah TR = PQ. Karena P = 2700 – 9Q2, diperoleh:
Untuk meminimumkan TR, bentuk persamaan . Dengan rumus turunan, diperoleh:
Dengan membuat , diperoleh persamaan:
2700 – 27Q2 = 0
100 – Q2 = 0
(10 + Q)(10 – Q) = 0
Q1 = -10 dan Q2 = 10 [Q = -10 atau Q = 10]
Di sini diperoleh dua buah titik stasioner, yaitu Q1 = -10 dan Q2 = 10. Untuk menentukan mana di antara kedua nilai ini yang menghasilkan TR maksimum, kita tentukan dulu TR”(Q) = , yaitu turunan dari terhadap Q. Dengan menggunakan rumus-rumus turunan, diperoleh:
Jika Q = -10 maka nilai turunan kedua TR terhadap Q adalah
Karena turunan kedua TR terhadap Q tersebut positif, nilai Q = -10 menghasilkan nilai minimum relatif total penerimaan.
Jika Q = 10 maka nilai turunan kedua TR terhadap Q adalah
Karena turunan kedua TR terhadap Q tersebut negatif, nilai Q = 10 menghasilkan nilai maksimum relatif total penerimaan.
Jadi, agar total penerimaan maksimum, banyaknya barang yang harus terjual adalah 10 unit.
Untuk menentukan berapa total penerimaan yang maksimum tersebut, substitusikan Q = 10 ke dalam (*2), diperoleh:
TR(10) = 2700.10 – 9.103 = 27000 – 9000 = 18000
Jadi, total penerimaan maksimumnya adalah Rp 18.000.
Contoh 3 (Memaksimumkan Laba)
Permintaan terhadap suatu produk memenuhi persamaan P = (90 – 3Q) rupiah/unit dan total biaya (TC, Total Cost) untuk menghasilkan Q unit produk tersebut adalah TC = Q3/10 – 3Q2 + 60Q + 100. Berapakah banyaknya produk yang harus dijual agar diperoleh laba maksimum? Berapakah laba maksimum tersebut?
Jawab:
Jika Q unit produk terjual maka penerimaan total (TR) yang terjadi adalah TR = PQ. Karena P = 90 – 3Q, diperoleh:
Untuk memaksimumkan π, bentuk persamaan . Dengan rumus turunan, diperoleh:
Dengan membuat , diperoleh persamaan:
Q2 – 100 = 0
(Q + 10)(Q – 10) = 0
Q1 = -10 dan Q2 = 10 [Q = -10 atau Q = 10]
Di sini diperoleh dua buah titik stasioner, yaitu Q1 = -10 dan Q2 = 10. Untuk menentukan mana di antara kedua nilai ini yang menghasilkan π maksimum, kita tentukan dulu π”(Q) = , yaitu turunan dari terhadap Q. Dengan menggunakan rumus-rumus turunan, diperoleh:
Jika Q = -10 maka nilai turunan kedua π terhadap Q adalah
Karena turunan kedua π terhadap Q tersebut positif, nilai Q = -10 menghasilkan nilai minimum relatif laba.
Jika Q = 10 maka nilai turunan kedua π terhadap Q adalah
Karena turunan kedua π terhadap Q tersebut negatif, nilai Q = 10 menghasilkan nilai maksimum relatif laba.
Jadi, agar laba mencapai nilai maksimum, banyaknya barang yang harus terjual adalah 10 unit.
Untuk menentukan berapa laba yang maksimum tersebut, substitusikan Q = 10 ke dalam (*3), diperoleh:
π(10) = – 103/10 + 30.10 – 100 = 100
Jadi, laba maksimumnya adalah Rp 100.
Contoh soal dan pembahasan: penerapan turunan dalam optimasi di bidang ekonomi (klik di sini)
PENERAPAN TURUNAN DALAM OPTIMASI DI BIDANG EKONOMI
Post kali ini menyajikan beberapa contoh bagaimana konsep turunan digunakan dalam optimasi di bidang ekonomi atau bisnis.
Contoh 1: (Meminimumkan Biaya Rata-rata)
Dalam produksi suatu barang, biaya totalnya adalah TC = (0,4Q2 + 500Q + 16000) rupiah. Berapakah banyaknya barang yang harus diproduksi agar biaya rata-ratanya (AC) minimum? Berapakah biaya rata-rata ninimum tersebut?
Jawab:
Biaya rata-rata (AC) dapat dinyatakan sebagai:
Untuk meminimumkan AC, bentuk persamaan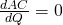 . Dengan rumus turunan, diperoleh:
. Dengan rumus turunan, diperoleh:
Dengan membuat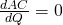 , diperoleh persamaan:
, diperoleh persamaan:
0,4 Q2 – 16000 = 0
Q2 – 40000 = 0
(Q+200)(Q-200) = 0
Q1 = -200 dan Q2 = 200 [Q = -200 atau Q = 200]
Di sini diperoleh dua buah titik stasioner, yaitu Q1 = -200 dan Q2 = 200. Untuk menentukan mana di antara kedua nilai ini yang menghasilkan AC minimum, kita tentukan dulu AC”(Q) = , yaitu turunan dari
, yaitu turunan dari  terhadap Q. Dengan menggunakan rumus-rumus turunan, diperoleh:
terhadap Q. Dengan menggunakan rumus-rumus turunan, diperoleh:
Jika Q = -200 maka nilai turunan kedua AC terhadap Q adalah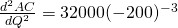
Karena turunan kedua AC terhadap Q tersebut negatif, nilai Q = -200 menghasilkan nilai maksimum relatif biaya rata-rata.
Jika Q = 200 maka nilai turunan kedua AC terhadap Q adalah:
Karena turunan kedua AC terhadap Q tersebut positif, nilai Q = 200 menghasilkan nilai minimum relatif biaya rata-rata.
Jadi, agar biaya rata-rata minimum, banyaknya barang yang harus diproduksi adalah 200 unit.
Untuk menentukan berapa biaya rata-rata yang minimum tersebut, substitusikan Q = 200 ke dalam (*1), diperoleh:
Jadi, biaya rata-rata minimumnya adalah Rp 660/unit.
Contoh 2 (Memaksimalkan Penerimaan Total)
Diketahui permintaan terhadap suatu produk mengikuti persamaan berikut: P = (2700 – 9Q2) rupiah/unit. Berapakah banyaknya produk yang harus terjual agar penerimaan total (TR, Total Revenue) dari hasil penjualan tersebut maksimum?
Jawab:
Jika Q unit produk terjual maka penerimaan total (TR) yang terjadi adalah TR = PQ. Karena P = 2700 – 9Q2, diperoleh:
TR(Q) = (2700 – 9Q2).Q
TR(Q) = 2700Q – 9Q3 ………………………………………………………………………………. (*2)
Untuk meminimumkan TR, bentuk persamaan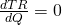 . Dengan rumus turunan, diperoleh:
. Dengan rumus turunan, diperoleh:
Dengan membuat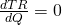 , diperoleh persamaan:
, diperoleh persamaan:
2700 – 27Q2 = 0
100 – Q2 = 0
(10 + Q)(10 – Q) = 0
Q1 = -10 dan Q2 = 10 [Q = -10 atau Q = 10]
Di sini diperoleh dua buah titik stasioner, yaitu Q1 = -10 dan Q2 = 10. Untuk menentukan mana di antara kedua nilai ini yang menghasilkan TR maksimum, kita tentukan dulu TR”(Q) =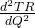 , yaitu turunan dari
, yaitu turunan dari 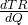 terhadap Q. Dengan menggunakan rumus-rumus turunan, diperoleh:
terhadap Q. Dengan menggunakan rumus-rumus turunan, diperoleh:
Jika Q = -10 maka nilai turunan kedua TR terhadap Q adalah
Karena turunan kedua TR terhadap Q tersebut positif, nilai Q = -10 menghasilkan nilai minimum relatif total penerimaan.
Jika Q = 10 maka nilai turunan kedua TR terhadap Q adalah
Karena turunan kedua TR terhadap Q tersebut negatif, nilai Q = 10 menghasilkan nilai maksimum relatif total penerimaan.
Jadi, agar total penerimaan maksimum, banyaknya barang yang harus terjual adalah 10 unit.
Untuk menentukan berapa total penerimaan yang maksimum tersebut, substitusikan Q = 10 ke dalam (*2), diperoleh:
TR(10) = 2700.10 – 9.103 = 27000 – 9000 = 18000
Jadi, total penerimaan maksimumnya adalah Rp 18.000.
Contoh 3 (Memaksimumkan Laba)
Permintaan terhadap suatu produk memenuhi persamaan P = (90 – 3Q) rupiah/unit dan total biaya (TC, Total Cost) untuk menghasilkan Q unit produk tersebut adalah TC = Q3/10 – 3Q2 + 60Q + 100. Berapakah banyaknya produk yang harus dijual agar diperoleh laba maksimum? Berapakah laba maksimum tersebut?
Jawab:
Jika Q unit produk terjual maka penerimaan total (TR) yang terjadi adalah TR = PQ. Karena P = 90 – 3Q, diperoleh:
TR(Q) = (90 – 3Q).Q
TR(Q) = 90Q – 3Q2
Selanjutnya, laba yang diperoleh (π), adalah
π = TR – TC
π(Q) = (90Q – 3Q2) – (Q3/10 – 3Q2 + 60Q + 100)
π(Q) = – Q3/10 + 30Q – 100 ……………………………………………………………………….. (*3)
Untuk memaksimumkan π, bentuk persamaan . Dengan rumus turunan, diperoleh:
. Dengan rumus turunan, diperoleh:
Dengan membuat , diperoleh persamaan:
, diperoleh persamaan:
Q2 – 100 = 0
(Q + 10)(Q – 10) = 0
Q1 = -10 dan Q2 = 10 [Q = -10 atau Q = 10]
Di sini diperoleh dua buah titik stasioner, yaitu Q1 = -10 dan Q2 = 10. Untuk menentukan mana di antara kedua nilai ini yang menghasilkan π maksimum, kita tentukan dulu π”(Q) =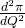 , yaitu turunan dari
, yaitu turunan dari 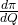 terhadap Q. Dengan menggunakan rumus-rumus turunan, diperoleh:
terhadap Q. Dengan menggunakan rumus-rumus turunan, diperoleh:
Jika Q = -10 maka nilai turunan kedua π terhadap Q adalah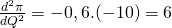
Karena turunan kedua π terhadap Q tersebut positif, nilai Q = -10 menghasilkan nilai minimum relatif laba.
Jika Q = 10 maka nilai turunan kedua π terhadap Q adalah
Karena turunan kedua π terhadap Q tersebut negatif, nilai Q = 10 menghasilkan nilai maksimum relatif laba.
Jadi, agar laba mencapai nilai maksimum, banyaknya barang yang harus terjual adalah 10 unit.
Untuk menentukan berapa laba yang maksimum tersebut, substitusikan Q = 10 ke dalam (*3), diperoleh:
π(10) = – 103/10 + 30.10 – 100 = 100
Jadi, laba maksimumnya adalah Rp 100.
Contoh soal dan pembahasan: penerapan turunan dalam optimasi di bidang ekonomi (klik di sini)
File presentasi: Applications of Derivatives in Business Optimization
Latihan Soal: Exercises on Application of Derivatives in Business Optimization
Bagikan ini:
Most visitors also read :
BERKENALAN DENGAN NILAI DAN VEKTOR EIGEN
DEKOMPOSISI NILAI SINGULAR (SINGULAR VALUE DECOMPOSITION)
MATRIKS AKAR KUADRAT
SOAL DAN PEMBAHASAN ANALISIS KOMPONEN UTAMA