MENYELESAIKAN PERSAMAAN KUADRAT DENGAN PEMFAKTORAN (1)

November 29th, 2016

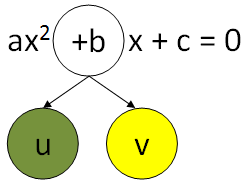
pk_faktor_0

Persamaan kuadrat memiliki bentuk umum ax² + bx + c = 0 dengan a ≠ 0. Berikut ini beberapa contoh persamaan kuadrat:

x² – 4x – 5 = 0 [a = 1, b = -4, c = -5]
-2x² – 3x + 9 = 0 [a = -2, b = -3, c = 9]
4x² + 7x = 0 [a = 4, b = 7, c = 0]
9x² – 16 = 0 [a = 9, b = 0, c = -16]

Suatu persamaan kuadrat dapat memiliki dua penyelesaian (dua akar), satu penyelesaian (satu akar/akar kembar), atau tidak memiliki akar, dalam arti: akarnya bukan merupakan bilangan nyata

Contoh 1 (dua akar berlainan)

x² – 4x – 5 = 0 memiliki dua penyelesaian yang berbeda, yaitu x = -1 atau x = 5. Perhatikan bahwa:

(-1)² -4(-1) – 5 = 1 + 4 – 5 = 0

dan 5² – 4.5 – 5 = 25 – 20 – 5 = 0

Contoh 2 (akar kembar)

x² – 6x + 9 = 0 hanya memiliki sebuah akar, yaitu x = 3. Perhatikan bahwa 3² – 6.3 + 9 = 9 – 18 + 9 = 0. Tidak ada nilai x lainnya yang memenuhi persamaan tersebut.

Contoh 3 (tidak memiliki akar)

x² + 100 = 0 tidak memiliki akar. Mengapa demikian? Agar ruas kiri bernilai nol, haruslah berlaku nilai x² = – 100. Tetapi ini tidak mungkin, karena kuadrat suatu bilangan nyata tidak mungkin bernilai negatif.

Bagaimana cara menemukan akar-akar tersebut?

Terdapat beberapa metode, namun dalam post kali ini akan dibahas metode pemfaktoran.

Jika persamaan kuadrat memiliki dua akar berlainan, penyelesaian persamaan tersebut menggunakan biimplikasi berikut ini:

[pq = 0] ⇔ [p = 0 atau q = 0] ………………………………………………………….. (+++)

Dari biimplikasi tersebut, dapat disimpulkan bahwa “jika hasil kali dua buah bilangan nyata (misalnya p dan q) bernilai nol maka ada di antara kedua bilangan tersebut yang bernilai nol.” Tidak mungkin terjadi p ≠ 0 dan q ≠ 0. Jadi, haruslah p = 0 atau q = 0.

Contoh 4

Tentukan penyelesaian dari persamaan 6x² – 5x – 4 = 0.

Jawab:

Karena 6x² – 5x – 4 = (3x – 4)(2x + 1), persamaan kuadrat tersebut dapat dinyatakan sebagai:

(3x – 4)(2x + 1) = 0 ………………………………………….. (*)

Ruas kiri (*) merupakan perkalian dua buah bilangan nyata, yaitu (3x – 4) dengan (2x + 1). Karena hasil kali keduanya ini bernilai nol, menurut biimplikasi di atas, harus ada di antara keduanya itu yang bernilai nol. Jadi, 3x – 4 = 0 atau 2x + 1 = 0. Karena 3x – 4 = 0 ⇔ $x = \frac{4}{3}$ dan 2x + 1 = 0 ⇔ $x = - \frac{1}{2}$ . Jadi, persamaan kuadrat tersebut memiliki dua penyelesaian, yaitu $x = \frac{4}{3}$ atau $x = - \frac{1}{2}$ .

Dalam penyelesaian persamaan kuadrat pada Contoh 4, 6x² – 5x – 4 dinyatakan dalam bentuk (3x – 4)(2x + 1). Proses “mengubah bentuk” 6x² – 5x – 4 menjadi (3x – 4)(2x + 1) dinamakan “memfaktorkan”. Bagaimanakah ini dilakukan? Inilah topik bahasan pada post kali ini.

Untuk memfaktorkan ax² + bx + c = 0, lakukan langkah-langkah berikut ini.

Langkah 1

Hitunglah perkalian ac.

Pada Contoh 4, a = 6 dan c = -4. Jadi, ac = 6(-4) = -24.

Langkah 2

Carilah dua buah bilangan u dan v sedemikian hingga uv = ac dan u + v = b.

pk_faktor_0

Pada Contoh 4, b = -5.

Sekarang kita cari dua buah bilangan u dan v sedemikian hingga uv = -24 dan u + v = -5. Dengan kata lain, kita mencari dua buah bilangan yang apabila dikalikan menghasilkan -24 dan apabila dijumlahkan menghasilkan -5. Kita temukan jawabannya, yaitu u = 3 dan v = -8.

pk_faktor_1

Langkah 3

Pada persamaan ax² + bx + c = 0, nyatakan bx sebagai penjumlahan antara ux dan vx.

pk_faktor_3

Pada Contoh 4 hal tersebut diterapkan sebagai berikut.

pk_faktor_2

6x² – 5x – 4 = 0 ⇔ 6x² + 3x + (-8x) – 4 = 0.

Langkah 4

Lakukan pemfaktoran terhadap (ax² + ux) dan (vx + c).

Pada Contoh 4, 6x² + 3x = 3x(2x + 1) dan (-8)x – 4 = -4(2x + 1), sehingga

6x² – 5x – 4 = 0

⇔ 6x² + 3x + (-8)x – 4 = 0

⇔ 3x(2x + 1) – 4(2x + 1) = 0

Langkah 5 (langkah akhir)

Faktorkan lagi hasil yang diperoleh pada Langkah 4.

Hasil yang diperoleh pada Langkah 4 Contoh 4 adalah: 3x(2x + 1) – 4(2x + 1) = 0. Ini dapat difaktorkan lagi menjadi: (2x + 1)(3x – 4) = 0.

Contoh 5

Tentukan penyelesaian dari persamaan -2x² – 3x + 9 = 0.

Jawab:

Untuk mencari penyelesaian persamaan tersebut, kita lakukan pemfaktoran terhadap -2x² – 3x + 9 menggunakan langkah-langkah yang telah dicontohkan tadi.

Langkah 1

Hitunglah perkalian ac.

Pada contoh ini, a = -2 dan c = 9. Jadi, ac = -2.9 = -18.

Langkah 2

Pada contoh ini, b = -3.

Carilah dua buah bilangan u dan v sedemikian hingga uv = -18 dan u + v = -3. Diperoleh u = -6 dan v = 3.

pk_faktor_4

Langkah 3

pk_faktor_5

Persamaan kuadrat tersebut dapat dinyatakan sebagai: -2x² – 6x + 3x + 9 = 0

Langkah 4

-2x² – 6x = -2x(x + 3)

3x + 9 = 3(x + 3)

Jadi, persamaan kuadrat tersebut dapat dinyatakan sebagai -2x(x+3) + 3(x+3) = 0

Langkah 5

Hasil yang diperoleh pada Langkah 4 Contoh 4 adalah: -2x(x+3) + 3(x+3) = 0. Lakukan pemfaktoran lagi pada ruas kiri, diperoleh:

(x+3)(-2x+3) = 0 …………………………………………………….. (**)

Sekarang, kita akan mencari akar-akar persamaan tersebut.

(**) menyatakan bahwa perkalian dua buah bilangan menghasilkan nol. Menurut (+++), ada di antara (x+3) dan (-2x+3) yang bernilai nol. Jadi, x + 3 = 0 atau -2x + 3 = 0.

Karena x + 3 = 0 ⇔ x = -3 dan -2x + 3 = 0 ⇔ $x = \frac{3}{2}$ .