Apabila suatu garis dan suatu lingkaran digambarkan pada bidang (datar) yang sama, terdapat tiga kemungkinan yang mungkin dalam hal banyaknya titik potong antara keduanya. Pertama, garis memotong lingkaran di dua titik berlainan. (Gambar 1)
Gambar 1
Kedua, garis tersebut dapat menyinggung lingkaran, memiliki hanya satu buah titik persekutuan. (Gambar 2) Titik persekutuan tersebut dinamakan titik singgung garis pada lingkaran. Garis itu sendiri dinamakan garis singgung.
Gambar 2
Ketiga, garis tersebut mungkin tidak memotong lingkaran. (Gambar 3)
Gambar 3
Misalkan persamaan lingkaran tersebut diketahui, yaitu x2 + y2 = R2. [Lingkaran ini berpusat di titik pangkat koordinat dan berjari-jari R.] Bagaimana cara menentukan persamaan dari garis singgung garis pada lingkaran?
Kasus 1: Gradien garis singgung tersebut diketahui, yaitu m.
Persamaan garis singgung ini adalah:
………………………………………………………. (1)
Contoh 1
Diketahui lingkaran dengan persamaan x2 + y2 = 9. Tentukan persamaan garis bergradien 2 yang menyinggung lingkaran tersebut. Tentukan pula koordinat titik-titik singgungnya!
Jawab:
Persamaan lingkaran tersebut dapat dinyatakan kembali sebagai x2 + y2 = 32. Jadi, jari-jari lingkaran ini adalah R = 3. Untuk menentukan persamaan garis singgung yang bergradien 2, substitusikan m = 2 dan R = 3 pada (1), diperoleh:
Ada dua garis yang menyinggung lingkaran tersebut, yaitu g1 dan g2 dengan persamaan masing-masing:
g1 ≡ y = 2x + 3√5
g2 ≡ y = 2x – 3√5
Gambar 4
Pada Gambar 4, P adalah titik singgung garis g1 pada lingkaran dan Q titik singgung g2 pada lingkaran. Untuk menentukan koordinat P, substitusikan y pada persamaan garis g1: y = 2x + 3√5 ke dalam persamaan lingkaran x2 + y2 = 9, diperoleh:
x2 + (2x + 3√5)2 = 9
⇔ 5x2 + 12x√5 + 36 = 0
Persamaan kuadrat ini memiliki akar kembar . Untuk mendapat ordinat P, substitusikan nilai x ini ke dalam persamaan g1, diperoleh:
Jadi,
Untuk menentukan koordinat Q, substitusikan y pada persamaan garis g2: y = 2x – 3√5 ke dalam persamaan lingkaran x2 + y2 = 9, diperoleh:
x2 + (2x – 3√5)2 = 9
⇔ 5x2 – 12x√5 + 36 = 0
Persamaan kuadrat ini memiliki akar kembar . Untuk mendapat ordinat Q, substitusikan nilai x ini ke dalam persamaan g2, diperoleh:
Jadi,
Bagaimana apabila lingkaran tersebut berpusat di (α,β)? Bagaimana menentukan persamaan garis singgung pada lingkaran ini yang bergradien m?
Persamaan garis singgung ini adalah:
…………………………………. (2)
Contoh 2
Misalkan L adalah sebuah lingkaran yang berpusat di (-4,1) dan berjari-jari 3. g1 dan g2 adalah garis-garis singgung pada L, yang bergradien 2. Tentukanlah persamaan kedua garis tersebut.
Jawab:
Pada kasus ini, α = -4, β = 1, R = 3, dan m = 2. Substitusikan keempat nilai ini ke dalam (2), diperoleh:
PERSAMAAN GARIS SINGGUNG PADA LINGKARAN (1)
Apabila suatu garis dan suatu lingkaran digambarkan pada bidang (datar) yang sama, terdapat tiga kemungkinan yang mungkin dalam hal banyaknya titik potong antara keduanya. Pertama, garis memotong lingkaran di dua titik berlainan. (Gambar 1)
Gambar 1
Kedua, garis tersebut dapat menyinggung lingkaran, memiliki hanya satu buah titik persekutuan. (Gambar 2) Titik persekutuan tersebut dinamakan titik singgung garis pada lingkaran. Garis itu sendiri dinamakan garis singgung.
Gambar 2
Ketiga, garis tersebut mungkin tidak memotong lingkaran. (Gambar 3)
Gambar 3
Misalkan persamaan lingkaran tersebut diketahui, yaitu x2 + y2 = R2. [Lingkaran ini berpusat di titik pangkat koordinat dan berjari-jari R.] Bagaimana cara menentukan persamaan dari garis singgung garis pada lingkaran?
Kasus 1: Gradien garis singgung tersebut diketahui, yaitu m.
Persamaan garis singgung ini adalah:
Contoh 1
Diketahui lingkaran dengan persamaan x2 + y2 = 9. Tentukan persamaan garis bergradien 2 yang menyinggung lingkaran tersebut. Tentukan pula koordinat titik-titik singgungnya!
Jawab:
Persamaan lingkaran tersebut dapat dinyatakan kembali sebagai x2 + y2 = 32. Jadi, jari-jari lingkaran ini adalah R = 3. Untuk menentukan persamaan garis singgung yang bergradien 2, substitusikan m = 2 dan R = 3 pada (1), diperoleh:
Ada dua garis yang menyinggung lingkaran tersebut, yaitu g1 dan g2 dengan persamaan masing-masing:
g1 ≡ y = 2x + 3√5
g2 ≡ y = 2x – 3√5
Gambar 4
Pada Gambar 4, P adalah titik singgung garis g1 pada lingkaran dan Q titik singgung g2 pada lingkaran. Untuk menentukan koordinat P, substitusikan y pada persamaan garis g1: y = 2x + 3√5 ke dalam persamaan lingkaran x2 + y2 = 9, diperoleh:
x2 + (2x + 3√5)2 = 9
⇔ 5x2 + 12x√5 + 36 = 0
Persamaan kuadrat ini memiliki akar kembar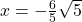 . Untuk mendapat ordinat P, substitusikan nilai x ini ke dalam persamaan g1, diperoleh:
. Untuk mendapat ordinat P, substitusikan nilai x ini ke dalam persamaan g1, diperoleh:
Jadi,
Untuk menentukan koordinat Q, substitusikan y pada persamaan garis g2: y = 2x – 3√5 ke dalam persamaan lingkaran x2 + y2 = 9, diperoleh:
x2 + (2x – 3√5)2 = 9
⇔ 5x2 – 12x√5 + 36 = 0
Persamaan kuadrat ini memiliki akar kembar . Untuk mendapat ordinat Q, substitusikan nilai x ini ke dalam persamaan g2, diperoleh:
. Untuk mendapat ordinat Q, substitusikan nilai x ini ke dalam persamaan g2, diperoleh:
Jadi,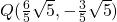
Bagaimana apabila lingkaran tersebut berpusat di (α,β)? Bagaimana menentukan persamaan garis singgung pada lingkaran ini yang bergradien m?
Persamaan garis singgung ini adalah:
Contoh 2
Misalkan L adalah sebuah lingkaran yang berpusat di (-4,1) dan berjari-jari 3. g1 dan g2 adalah garis-garis singgung pada L, yang bergradien 2. Tentukanlah persamaan kedua garis tersebut.
Jawab:
Pada kasus ini, α = -4, β = 1, R = 3, dan m = 2. Substitusikan keempat nilai ini ke dalam (2), diperoleh:
Jadi, persamaan-persamaan g1 dan g2 adalah:
g1 ≡ y = 2x + (9 + 3√5)
g2 ≡ y = 2x + (9 – 3√5)
Gambar 5
(bersambung)
Bagikan ini:
Most visitors also read :
BERKENALAN DENGAN NILAI DAN VEKTOR EIGEN
DEKOMPOSISI NILAI SINGULAR (SINGULAR VALUE DECOMPOSITION)
MATRIKS AKAR KUADRAT
SOAL DAN PEMBAHASAN ANALISIS KOMPONEN UTAMA