Misalkan diketahui limas segitiga T.ABC. Pada limas tersebut, misalkan D adalah titik tengah BC, E titik tengah AB. Titik potong antara AD dan CE adalah F, yaitu titik berat ΔABC. Karena itu CF:FE = 2:1 (untuk pembuktian mengenai perbandingan ini, silakan pelajari materi Titik Berat Segitiga). Tarik garis yang melalui T dan F, sehingga TF merupakan suatu garis berat limas tersebut. (Lihat gambar di bawah.)
Karena E titik tengah AB, TE merupakan suatu garis berat ΔTAB. Misalkan K titik tengah TB. Dengan demikian AK merupakan garis berat lainnya dari ΔTAB. TE dan AK saling berpotongan di G, yaitu titik berat ΔTAB. Karena itu EG:GT = 1:2 (untuk pembuktian mengenai perbandingan ini, silakan pelajari materi Titik Berat Segitiga). Kemudian tarik garis yang melalui C dan G, sehingga CG merupakan garis berat lainnya dari limas tersebut. Karena CG dan TF keduanya terletak di ΔTEC dan keduanya tidak sejajar, kedua garis tersebut akan berpotongan di suatu titik, misalkan titik P. Titik P ini merupakan titik berat limas T.ABC. Berapa perbandingan TP:PF? Berapa perbandingan CP:PG? Inilah yang akan kita jawab.
Sekarang, misalkan , , .
Misalkan juga dan (0 < x < 1 dan 0 < y < 1).
Akibatnya, .
Perhatikan bahwa . Dari perbandingan CF:FE = 2:1 diperoleh bahwa . Jadi, dapat dinyatakan sebagai:
Dari perbandingan EG:GT = 1:2 dan CF:FE = 2:1, diperoleh:
………………………. (*)
Substitusikan , , dan ke dalam (*) akan diperoleh persamaan vektor: .
Perhatikan bahwa tidak dapat dinyatakan sebagai kombinasi linier dari dan . Selain itu, dan tidak sejajar. Dari dua pernyataan tersebut, kita simpulkan bahwa , dan saling bebas. Karena ketiga vektor ini saling bebas, mensyaratkan ketiga hal berikut:
Solusi sistem persamaan linier tersebut menghasilkan .
Jadi, TP:PF = CP:PG = 3:1.
Pertanyaan selanjutnya sekarang adalah apabila koordinat T, A, B, dan C diketahui, berapakah koordinat titik beratnya? Dari perbandingan TP:PF = 3:1, diperoleh bahwa . Dengan notasi vektor posisi dari titik F, P, dan T, diperoleh:
…………………………………………………………………….. (**)
Dari perbandingan CF:FE = 2:1, diperoleh bahwa sehingga (**) dapat dinyatakan sebagai:
Karena E titik tengah AB, sehingga diperoleh .
Contoh:
Diketahui limas T.ABC dengan T(3,6,8), A(3,-2,0), B(7,1,0), dan C(-5,3,0). Tentukan koordinat titik berat limas tersebut.
Jawab:
Misalkan titik berat limas tersebut adalah P.
Jadi, koodinat titik berat limas tersebut adalah (2,2,2).
TITIK BERAT LIMAS SEGITIGA
Misalkan diketahui limas segitiga T.ABC. Pada limas tersebut, misalkan D adalah titik tengah BC, E titik tengah AB. Titik potong antara AD dan CE adalah F, yaitu titik berat ΔABC. Karena itu CF:FE = 2:1 (untuk pembuktian mengenai perbandingan ini, silakan pelajari materi Titik Berat Segitiga). Tarik garis yang melalui T dan F, sehingga TF merupakan suatu garis berat limas tersebut. (Lihat gambar di bawah.)
Karena E titik tengah AB, TE merupakan suatu garis berat ΔTAB. Misalkan K titik tengah TB. Dengan demikian AK merupakan garis berat lainnya dari ΔTAB. TE dan AK saling berpotongan di G, yaitu titik berat ΔTAB. Karena itu EG:GT = 1:2 (untuk pembuktian mengenai perbandingan ini, silakan pelajari materi Titik Berat Segitiga). Kemudian tarik garis yang melalui C dan G, sehingga CG merupakan garis berat lainnya dari limas tersebut. Karena CG dan TF keduanya terletak di ΔTEC dan keduanya tidak sejajar, kedua garis tersebut akan berpotongan di suatu titik, misalkan titik P. Titik P ini merupakan titik berat limas T.ABC. Berapa perbandingan TP:PF? Berapa perbandingan CP:PG? Inilah yang akan kita jawab.
Sekarang, misalkan ,
,  ,
,  .
.
Misalkan juga dan
dan 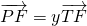 (0 < x < 1 dan 0 < y < 1).
(0 < x < 1 dan 0 < y < 1).
Akibatnya, .
.
Perhatikan bahwa . Dari perbandingan CF:FE = 2:1 diperoleh bahwa
. Dari perbandingan CF:FE = 2:1 diperoleh bahwa 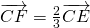 . Jadi,
. Jadi,  dapat dinyatakan sebagai:
dapat dinyatakan sebagai:
Dari perbandingan EG:GT = 1:2 dan CF:FE = 2:1, diperoleh:
Substitusikan ,
,  , dan
, dan  ke dalam (*) akan diperoleh persamaan vektor:
ke dalam (*) akan diperoleh persamaan vektor: 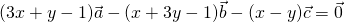 .
.
Perhatikan bahwa tidak dapat dinyatakan sebagai kombinasi linier dari
tidak dapat dinyatakan sebagai kombinasi linier dari  dan
dan 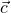 . Selain itu,
. Selain itu,  dan
dan 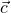 tidak sejajar. Dari dua pernyataan tersebut, kita simpulkan bahwa
tidak sejajar. Dari dua pernyataan tersebut, kita simpulkan bahwa  ,
,  dan
dan 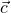 saling bebas. Karena ketiga vektor ini saling bebas,
saling bebas. Karena ketiga vektor ini saling bebas,  mensyaratkan ketiga hal berikut:
mensyaratkan ketiga hal berikut:
Solusi sistem persamaan linier tersebut menghasilkan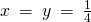 .
.
Jadi, TP:PF = CP:PG = 3:1.
Pertanyaan selanjutnya sekarang adalah apabila koordinat T, A, B, dan C diketahui, berapakah koordinat titik beratnya? Dari perbandingan TP:PF = 3:1, diperoleh bahwa . Dengan notasi vektor posisi dari titik F, P, dan T, diperoleh:
. Dengan notasi vektor posisi dari titik F, P, dan T, diperoleh:
Dari perbandingan CF:FE = 2:1, diperoleh bahwa sehingga (**) dapat dinyatakan sebagai:
sehingga (**) dapat dinyatakan sebagai:
Karena E titik tengah AB, sehingga diperoleh
sehingga diperoleh  .
.
Contoh:
Diketahui limas T.ABC dengan T(3,6,8), A(3,-2,0), B(7,1,0), dan C(-5,3,0). Tentukan koordinat titik berat limas tersebut.
Jawab:
Misalkan titik berat limas tersebut adalah P.
Jadi, koodinat titik berat limas tersebut adalah (2,2,2).
Bagikan ini:
Most visitors also read :
BERKENALAN DENGAN NILAI DAN VEKTOR EIGEN
DEKOMPOSISI NILAI SINGULAR (SINGULAR VALUE DECOMPOSITION)
MATRIKS AKAR KUADRAT
SOAL DAN PEMBAHASAN ANALISIS KOMPONEN UTAMA