Bagaimanakah menggambar grafik fungsi untuk 0 ≤ x ≤ 2π? Apabila kita telah mengetahui grafik fungsi y = sin x, maka dengan teknik-teknik yang diajarkan berikut ini, grafik fungsi tersebut dapat dengan mudah digambarkan. Sebelum kita mencari jawaban untuk soal tersebut, mari kita pelajari terlebih dahulu “teori-teori” berikut.
[P1] Mendapatkan y = sin kx dari y = sin x
Perkalian variabel bebas dengan konstanta k berpengaruh terhadap periode fungsi trigonometri tersebut. y = sin x memiliki periode 2π, sedangkan y = sin kx memiliki periode .
Mari kita bandingkan grafik y = sin x (Gambar 1a) dengan y = sin 2x (Gambar 1b). y = sin x memiliki periode 2π, sedangkan y = sin 2x memiliki periode π.
Gambar 1a
Gambar 1b
memiliki periode (Gambar 1c)
Gambar 1bGambar 1c
Namun hati-hati apabila k < 0. Apabila k < 0, kita terapkan rumus sin (-α) = – sin α. Jadi, untuk menggambar grafik y = sin (-2x), kita “ingat” bahwa sin (-2x) = – sin 2x, sehingga grafik y = sin (-2x) akan sama dengan grafik y = – sin 2x. Perhatikan Gambar 1d, yaitu grafik y = sin (-2x) dan bandingkan dengan Gambar 1b yang merupakan grafik y = sin 2x.
Gambar 1d
Demikian pula misalnya: y = cos x memiliki periode 2π sedangkan y = cos 2x memiliki periode π. Lihat Gambar 1e, grafik y = cos 2x.
Gambar 1e
Bandingkan dengan Gambar 1f yang merupakan grafik fungsi y = cos x.
Gambar 1f
[P2] Mendapatkan y = A sin x dari y = sin x
Perkalian sin x dengan A berpengaruh pada “ketinggian” grafik. Bandingkan grafik y = sin x, grafik y = 2 sin x, dan grafik y = ½ sin x pada Gambar 2a.
Gambar 2a
Namun hati-hati apabila A < 0. Jika A < 0, grafik y = A sin x diperoleh dengan “mencerminkan” grafik y = (-A) sin x terhadap sumbu x. Jadi, grafik y = -2 sin x dapat diperoleh dengan cara mencerminkan grafik y = 2 sin x terhadap sumbu x. (Gambar 2b)
Gambar 2b
[P3] Mendapatkan y = sin (x±θ) dari y = sin x
Grafik y = sin (x – π/3) dapat diperoleh dengan cara “menggeser” atau men-translasikan kurva sejauh π/3 searah dengan arah sumbu x positif. Lihat Gambar 3a.
Gambar 3a
Grafik y = sin (x + π/3) dapat diperoleh dengan cara “menggeser” atau men-translasikan kurva sejauh π/3 searah dengan arah sumbu x negatif. Lihat Gambar 3b.
Gambar 3b
Sekarang, bagaimana menggambar y = sin (2x – π/3)?
y = sin (2x – π/3) dapat dinyatakan sebagai y = sin 2(x – π/6). Jadi, kurva y = sin (2x – π/3) dapat diperoleh dengan menggeser kurva y = 2x sejauh π/6 searah dengan sumbu x positif.
Gambar 3c
Teknik semacam ini berlaku juga untuk y = cos (x±θ). Bandingkan kurva y = cos x dengan y = cos (x-π/4) pada Gambar 3d.
Gambar 3d
[P4] Mendapatkan y = b + sin x dari y = sin x
Grafik y = b + sin x diperoleh dengan “mengangkat” atau “menurunkan” grafik y = sin x sejauh b satuan sejajar dengan sumbu y. Jika b > 0 grafik y = b + sin x diperoleh dengan menggeser grafik y = sin x sejauh b satuan searah dengan sumbu y positif. Jika b < 0 grafik y = b + sin x diperoleh dengan menggeser grafik y = sin x sejauh b satuan searah dengan sumbu y negatif.
Pada Gambar 4, dapat dilihat pengaruh penambahan konstanta b pada sin x sebagaimana dimaksudkan di atas. Perhatikan perbedaan antara grafik y = sin x, grafik y = ¾ + sin x, dan grafik y = -¾ + sin x.
Gambar 4
Kembali ke pertanyaan di awal post ini: bagaimana menggambar grafik fungsi ? Kita perlu terlebih dahulu menelusuri “sejarah” perubahan y = sin x menjadi . Sejarah tersebut dapat diilustrasikan dalam bagan berikut.
Gambar 5
Sebagai langkah awal, kita gambarkan terlebih dahulu y = sin x untuk 0 ≤ x ≤ 2π. (Gambar 1a)
Perubahan [P1]: Periode berubah menjadi 2π/3 (Gambar 6)
Gambar 6
Perubahan [P2]: Kurva menjadi “lebih tinggi” menjadi 2 kali lipat dari semula (Gambar 7)
Gambar 7
Perubahan [P3]:
y = 2 sin (3x – π/4) dapat dinyatakan sebagai y = 2 sin 3(x – π/12). Jadi, kurva y = 2 sin (3x – π/4) dapat diperoleh dengan cara mentranslasikan kurva y = 2 sin 3x sejauh π/12 searah dengan arah sumbu x positif. (Gambar 8)
Gambar 8
Perubahan [P4]: Kurva “turun” sejauh 1 satuan (Gambar 9)
Gambar 9
Jadi, grafik y = -1 + 2 sin (3x – π/4) adalah sebagai berikut (yaitu kurva merah pada Gambar 9):
MENGGAMBAR GRAFIK FUNGSI TRIGONOMETRI
Bagaimanakah menggambar grafik fungsi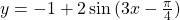
untuk 0 ≤ x ≤ 2π? Apabila kita telah mengetahui grafik fungsi y = sin x, maka dengan teknik-teknik yang diajarkan berikut ini, grafik fungsi tersebut dapat dengan mudah digambarkan. Sebelum kita mencari jawaban untuk soal tersebut, mari kita pelajari terlebih dahulu “teori-teori” berikut.
[P1] Mendapatkan y = sin kx dari y = sin x
Perkalian variabel bebas dengan konstanta k berpengaruh terhadap periode fungsi trigonometri tersebut. y = sin x memiliki periode 2π, sedangkan y = sin kx memiliki periode
.
Mari kita bandingkan grafik y = sin x (Gambar 1a) dengan y = sin 2x (Gambar 1b). y = sin x memiliki periode 2π, sedangkan y = sin 2x memiliki periode π.
Gambar 1a
Gambar 1b
Gambar 1b
Gambar 1c
Namun hati-hati apabila k < 0. Apabila k < 0, kita terapkan rumus sin (-α) = – sin α. Jadi, untuk menggambar grafik y = sin (-2x), kita “ingat” bahwa sin (-2x) = – sin 2x, sehingga grafik y = sin (-2x) akan sama dengan grafik y = – sin 2x. Perhatikan Gambar 1d, yaitu grafik y = sin (-2x) dan bandingkan dengan Gambar 1b yang merupakan grafik y = sin 2x.
Gambar 1d
Demikian pula misalnya: y = cos x memiliki periode 2π sedangkan y = cos 2x memiliki periode π. Lihat Gambar 1e, grafik y = cos 2x.
Gambar 1e
Bandingkan dengan Gambar 1f yang merupakan grafik fungsi y = cos x.
Gambar 1f
[P2] Mendapatkan y = A sin x dari y = sin x
Perkalian sin x dengan A berpengaruh pada “ketinggian” grafik. Bandingkan grafik y = sin x, grafik y = 2 sin x, dan grafik y = ½ sin x pada Gambar 2a.
Gambar 2a
Namun hati-hati apabila A < 0. Jika A < 0, grafik y = A sin x diperoleh dengan “mencerminkan” grafik y = (-A) sin x terhadap sumbu x. Jadi, grafik y = -2 sin x dapat diperoleh dengan cara mencerminkan grafik y = 2 sin x terhadap sumbu x. (Gambar 2b)
Gambar 2b
[P3] Mendapatkan y = sin (x±θ) dari y = sin x
Grafik y = sin (x – π/3) dapat diperoleh dengan cara “menggeser” atau men-translasikan kurva sejauh π/3 searah dengan arah sumbu x positif. Lihat Gambar 3a.
Gambar 3a
Grafik y = sin (x + π/3) dapat diperoleh dengan cara “menggeser” atau men-translasikan kurva sejauh π/3 searah dengan arah sumbu x negatif. Lihat Gambar 3b.
Gambar 3b
Sekarang, bagaimana menggambar y = sin (2x – π/3)?
y = sin (2x – π/3) dapat dinyatakan sebagai y = sin 2(x – π/6). Jadi, kurva y = sin (2x – π/3) dapat diperoleh dengan menggeser kurva y = 2x sejauh π/6 searah dengan sumbu x positif.
Gambar 3c
Teknik semacam ini berlaku juga untuk y = cos (x±θ). Bandingkan kurva y = cos x dengan y = cos (x-π/4) pada Gambar 3d.
Gambar 3d
[P4] Mendapatkan y = b + sin x dari y = sin x
Grafik y = b + sin x diperoleh dengan “mengangkat” atau “menurunkan” grafik y = sin x sejauh b satuan sejajar dengan sumbu y. Jika b > 0 grafik y = b + sin x diperoleh dengan menggeser grafik y = sin x sejauh b satuan searah dengan sumbu y positif. Jika b < 0 grafik y = b + sin x diperoleh dengan menggeser grafik y = sin x sejauh b satuan searah dengan sumbu y negatif.
Pada Gambar 4, dapat dilihat pengaruh penambahan konstanta b pada sin x sebagaimana dimaksudkan di atas. Perhatikan perbedaan antara grafik y = sin x, grafik y = ¾ + sin x, dan grafik y = -¾ + sin x.
Gambar 4
Kembali ke pertanyaan di awal post ini: bagaimana menggambar grafik fungsi
? Kita perlu terlebih dahulu menelusuri “sejarah” perubahan y = sin x menjadi 
. Sejarah tersebut dapat diilustrasikan dalam bagan berikut.
Gambar 5
Sebagai langkah awal, kita gambarkan terlebih dahulu y = sin x untuk 0 ≤ x ≤ 2π. (Gambar 1a)
Perubahan [P1]: Periode berubah menjadi 2π/3 (Gambar 6)
Gambar 6
Perubahan [P2]: Kurva menjadi “lebih tinggi” menjadi 2 kali lipat dari semula (Gambar 7)
Gambar 7
Perubahan [P3]:
y = 2 sin (3x – π/4) dapat dinyatakan sebagai y = 2 sin 3(x – π/12). Jadi, kurva y = 2 sin (3x – π/4) dapat diperoleh dengan cara mentranslasikan kurva y = 2 sin 3x sejauh π/12 searah dengan arah sumbu x positif. (Gambar 8)
Gambar 8
Perubahan [P4]: Kurva “turun” sejauh 1 satuan (Gambar 9)
Gambar 9
Jadi, grafik y = -1 + 2 sin (3x – π/4) adalah sebagai berikut (yaitu kurva merah pada Gambar 9):
Gambar 10
Bagikan ini:
Most visitors also read :
BERKENALAN DENGAN NILAI DAN VEKTOR EIGEN
DEKOMPOSISI NILAI SINGULAR (SINGULAR VALUE DECOMPOSITION)
MATRIKS AKAR KUADRAT
SOAL DAN PEMBAHASAN ANALISIS KOMPONEN UTAMA