Di post saya sebelumnya telah diterangkan bahwa ada tiga statistik yang dapat digunakan untuk melakukan uji hipotesis dua-sampel mengenai rata-rata. Ketiga statistik tersebut adalah sebagai berikut.
Penggunaan (1) dan (2) telah dibahas pada post sebelumnya. Post ini membahas penggunaan (3).
Rumus (3)
Statistik ini berdistribusi t dengan derajat kebebasan:
Nilai df yang diperoleh biasanya dibulatkan ke bawah, sampai bilangan bulat terdekat.
Syarat penggunaan:
Kedua sampel diambil dari populasi yang masing-masing berdistribusi normal.
Simpangan baku atau variansi kedua populasi tidak diketahui, namun tidak sama nilainya.
Kedua sampel saling bebas, tidak saling berhubungan.
Contoh 3
Terdapat dua acara serupa yang disiarkan di dua stasiun radio yang berbeda, yaitu stasiun radio A dan stasiun radio B. Terdapat suatu dugaan bahwa pendengar acara tersebut di stasiun radio A lebih lama mengikuti acara tersebut daripada pendengar acara serupa di stasiun radio B. Untuk memeriksa hal ini, diambillah secara acak 10 orang pendengar acara tersebut di stasiun radio A dan diperoleh rata-rata lamanya mendengarkan acara tersebut adalah 45 menit dengan simpangan baku 6 menit. Dari populasi pendengar acara tersebut di stasiun radio B diambil pula sampel acak berukuran 15 dan diperoleh rata-rata lamanya mendengarkan acara tersebut adalah 42 menit dengan simpangan baku 3 menit. Apakah sampel yang diambil ini mendukung pernyataan bahwa pendengar acara tersebut di stasiun radio A lebih lama mengikuti acara tersebut daripada pendengar acara serupa di stasiun radio B? Gunakan taraf nyata 0,05. Anggaplah kedua populasi berdistribusi normal dengan simpangan baku yang berbeda.
Jawab:
Misalkan
Rata-rata lamanya mendengarkan acara tersebut di stasiun radio A adalah μA.
Rata-rata lamanya mendengarkan acara tersebut di stasiun radio B adalah μB.
Pada contoh ini, , nA = 10, sA = 6 menit, , nB = 15, sB = 3 menit. α = 0,05.
Langkah 1 dan 2
H0: μA = μB
H1: μA > μB
Pasangan hipotesis tersebut dapat ditulis kembali sebagai berikut.
H0: μA – μB = 0
H1: μA – μB > 0
Langkah 3
α = 0,05
Langkah 4
Pada contoh ini, kedua simpangan baku sampel diketahui, masing-masing populasi berdistribusi normal, sampel-sampel ini saling bebas, dan simpangan baku kedua populasi berbeda. Jadi rumus (3) dapat digunakan. Untuk menentukan daerah kritis, peru dihitung dulu derajat kebebasan. Substitusikan nilai-nilai yang sudah diketahui ke dalam rumus df di atas, diperoleh:
Hasil di atas dibulatkan ke bawah hingga bilangan bulat terdekat. Jadi, df ≈ 12.
Daerah kritisnya adalah t > t0,05;12. Dari tabel nilai kritis t, diperoleh daerah kritis t > 1,782 (lihat gambar di bawah.)
Langkah 5
Substitusikan nilai-nilai yang telah diketahui ke dalam (3), diperoleh:
Langkah 6
Karena statistik uji pada Langkah 5 jatuh di daerah penerimaan, kita tak dapat menolak H0. Jadi, sampel tersebut tidak mendukung pernyataan bahwa pendengar acara tersebut di stasiun radio A lebih lama mengikuti acara tersebut daripada pendengar acara serupa di stasiun radio B.Bukti yang telah diperoleh tidak cukup untuk menyimpulkan bahwa pendengar acara tersebut di stasiun radio A lebih lama mengikuti acara tersebut daripada pendengar acara serupa di stasiun radio B.
UJI HIPOTESIS DUA-SAMPEL (3)
Di post saya sebelumnya telah diterangkan bahwa ada tiga statistik yang dapat digunakan untuk melakukan uji hipotesis dua-sampel mengenai rata-rata. Ketiga statistik tersebut adalah sebagai berikut.
Penggunaan (1) dan (2) telah dibahas pada post sebelumnya. Post ini membahas penggunaan (3).
Rumus (3)
Statistik ini berdistribusi t dengan derajat kebebasan:
Nilai df yang diperoleh biasanya dibulatkan ke bawah, sampai bilangan bulat terdekat.
Syarat penggunaan:
Contoh 3
Terdapat dua acara serupa yang disiarkan di dua stasiun radio yang berbeda, yaitu stasiun radio A dan stasiun radio B. Terdapat suatu dugaan bahwa pendengar acara tersebut di stasiun radio A lebih lama mengikuti acara tersebut daripada pendengar acara serupa di stasiun radio B. Untuk memeriksa hal ini, diambillah secara acak 10 orang pendengar acara tersebut di stasiun radio A dan diperoleh rata-rata lamanya mendengarkan acara tersebut adalah 45 menit dengan simpangan baku 6 menit. Dari populasi pendengar acara tersebut di stasiun radio B diambil pula sampel acak berukuran 15 dan diperoleh rata-rata lamanya mendengarkan acara tersebut adalah 42 menit dengan simpangan baku 3 menit. Apakah sampel yang diambil ini mendukung pernyataan bahwa pendengar acara tersebut di stasiun radio A lebih lama mengikuti acara tersebut daripada pendengar acara serupa di stasiun radio B? Gunakan taraf nyata 0,05. Anggaplah kedua populasi berdistribusi normal dengan simpangan baku yang berbeda.
Jawab:
Misalkan
Rata-rata lamanya mendengarkan acara tersebut di stasiun radio A adalah μA.
Rata-rata lamanya mendengarkan acara tersebut di stasiun radio B adalah μB.
Pada contoh ini, , nA = 10, sA = 6 menit,
, nA = 10, sA = 6 menit, 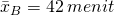 , nB = 15, sB = 3 menit. α = 0,05.
, nB = 15, sB = 3 menit. α = 0,05.
Langkah 1 dan 2
H0: μA = μB
H1: μA > μB
Pasangan hipotesis tersebut dapat ditulis kembali sebagai berikut.
H0: μA – μB = 0
H1: μA – μB > 0
Langkah 3
α = 0,05
Langkah 4
Pada contoh ini, kedua simpangan baku sampel diketahui, masing-masing populasi berdistribusi normal, sampel-sampel ini saling bebas, dan simpangan baku kedua populasi berbeda. Jadi rumus (3) dapat digunakan. Untuk menentukan daerah kritis, peru dihitung dulu derajat kebebasan. Substitusikan nilai-nilai yang sudah diketahui ke dalam rumus df di atas, diperoleh:
Hasil di atas dibulatkan ke bawah hingga bilangan bulat terdekat. Jadi, df ≈ 12.
Daerah kritisnya adalah t > t0,05;12. Dari tabel nilai kritis t, diperoleh daerah kritis t > 1,782 (lihat gambar di bawah.)
Langkah 5
Substitusikan nilai-nilai yang telah diketahui ke dalam (3), diperoleh:
Langkah 6
Karena statistik uji pada Langkah 5 jatuh di daerah penerimaan, kita tak dapat menolak H0. Jadi, sampel tersebut tidak mendukung pernyataan bahwa pendengar acara tersebut di stasiun radio A lebih lama mengikuti acara tersebut daripada pendengar acara serupa di stasiun radio B. Bukti yang telah diperoleh tidak cukup untuk menyimpulkan bahwa pendengar acara tersebut di stasiun radio A lebih lama mengikuti acara tersebut daripada pendengar acara serupa di stasiun radio B.
Uji t Berpasangan (Paired t Test)
materi dalam format pdf: (klik di sini)
youtube channel: (klik di sini)
latihan soal: (klik di sini)
pembahsan latihan soal: (klik di sini)
Latihan Soal
Latihan Penggunaan Rumus 1 s.d. 3 (Hanya no. 1 s.d. no. 8. Nomor 9 dan 10 tentang Uji t Berpasangan)
Latihan Penggunaan Rumus 2 dan 3 dan cara penyelesaiannya.
File Presentasi:
Uji Hipotesis 2-Sampel
Bagikan ini:
Most visitors also read :
DEKOMPOSISI NILAI SINGULAR (SINGULAR VALUE DECOMPOSITION)
MAXIMUM LIKELIHOOD ESTIMATOR
JARAK STATISTIKAL
SOAL DAN PEMBAHASAN ANALISIS KOMPONEN UTAMA