TURUNAN KIRI DAN TURUNAN KANAN SUATU FUNGSI
Di post saya yang lain, saya telah menerangkan konsep limit kiri dan limit kanan, dan hubungannya dengan eksistensi limit fungsi di suatu titik. Dikatakan bahwa limit fungsi di suatu titik ada jika dan hanya jika nilai limit kirinya sama dengan limit kanannya. Serupa dengan itu, turunan fungsi di suatu titik dijamin eksistensinya jika dan hanya jika nilai turunan kirinya sama dengan nilai turunan kanannya.
Turunan Kiri
Misalkan f merupakan suatu fungsi yang terdefinisi pada selang (a,c]. Turunan kiri f di x = c, ditulis f–‘(c), didefinisikan sebagai berikut.
![]()
jika limit tersebut ada.
Secara ekivalen, (1) dapat dinyatakan sebagai:
![]()
Turunan Kanan
Misalkan f merupakan suatu fungsi yang terdefinisi pada selang [c,b). Turunan kanan f di x = c, ditulis f+‘(c), didefinisikan sebagai berikut.
![]()
jika limit tersebut ada.
Secara ekivalen, (2) dapat dinyatakan sebagai:
![]()
Hubungan antara turunan kiri dan turunan kanan dengan keterdiferensialan fungsi di suatu titik dinyatakan dengan teorema berikut.
Teorema
Misalkan fungsi f terdefinisi pada suatu selang terbuka (a,b). Misalkan c ∊ (a,b).
f memiliki turunan di c jika dan hanya jika f–‘(c) = f+’(c).
Contoh 1
Perhatikan fungsi riil f yang didefinisikan pada ℝ yang aturan fungsinya adalah f(x) = x.|x| – 4x. Hitunglah turunan kiri dan turunan kanan f di x = 0. Apakah f terdiferensialkan di x = 0?
Jawab:
Pilih suatu selang terbuka yang memuat x = 0, misalnya (-1,1). Jika x ≥ 0 maka |x| = x dan selanjutnya f(x) dapat dinyatakan sebagai f(x) = x2 – 4x. Namun jika x < 0 maka |x| = -x dan selanjutnya f(x) = -x2 – 4x. Jadi, f(x) dapat dinyatakan sebagai:
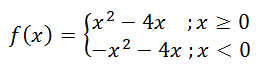
Dengan (1), turunan kiri f di x = 0 dihitung sebagai berikut:
![]()
Karena x menuju dari kiri 0, nilai x senantiasa negatif sehingga f(x) = -x2 – 4x. Substitusikan ini ke dalam (*), diperoleh:
![]()
Dengan (2), turunan kanan f di x = 0 dihitung sebagai berikut:
![]()
Karena x menuju dari kanan 0, nilai x senantiasa positif sehingga f(x) = x2 – 4x. Substitusikan ini ke dalam (**), diperoleh:
![]()
Karena f–‘(0) = f+’(0), kita simpulkan bahwa f terdiferensialkan di x = 0.
Contoh 2
Perhatikan fungsi riil g yang didefinisikan pada ℝ yang aturan fungsinya adalah:
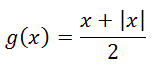
Hitunglah turunan kiri dan turunan kanan g di x = 0. Apakah g terdiferensialkan di x = 0?
Jawab:
Perhatikan bahwa g(x) dapat dinyatakan sebagai:
![]()
Pilih suatu selang terbuka yang memuat x = 0, misalnya (-1,1).
Dengan menggunakan (1), turunan kiri g di x = 0 dapat dihitung sebagai berikut:
![]()
Karena x menuju dari kiri 0, nilai x senantiasa negatif sehingga g(x) = 0. Substitusikan ini ke dalam (+), diperoleh:
![]()
Dengan menggunakan (2), turunan kanan g di x = 0 dihitung sebagai berikut:
![]()
Karena x menuju dari kanan 0, nilai x senantiasa positif sehingga g(x) = x. Substitusikan ini ke dalam (++), diperoleh:
![]()
Karena g–‘(0) ≠ g+’(0), kita simpulkan bahwa g tidak terdiferensialkan di x = 0.
Apabila digambarkan pada bidang Kartesius, grafik fungsi g adalah sebagai berikut.

Gambar 1
Bandingkanlah dengan grafik f pada Gambar 2:
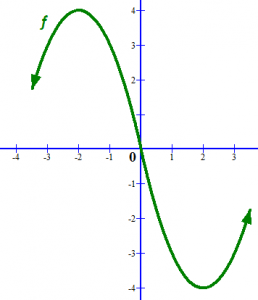
Gambar 2
Dengan membandingkan kedua gambar tersebut, saya berharap Anda memiliki suatu pemahaman tertentu mengenai perbedaan antara fungsi yang terdiferensialkan di suatu titik dengan yang tidak terdiferensialkan.
Tagging: terdiferensialkan, turunan kanan, turunan kiri



Itu kode [pmath]-nya gak jalan…