Di post saya yang lalu telah diuraikan bahwa ada tiga rumus yang dapat digunakan untuk menaksir rata-rata populasi dengan derajat kepercayaan tertentu:
Pada post ini akan dibahas penggunaan rumus (2) dan (3).
Syarat Penggunaan Rumus (2)
Simpangan baku populasi (σ) diketahui
Populasi berdistribusi normal atau n ≥ 30
Langkah-langkah Penggunaan Rumus (2)
Hitunglah α = 1 – γ dan α/2. γ menyatakan derajat kepercayaan.
Dengan menggunakan tabel luas daerah di bawah kurva normal baku, carilah nilai zα/2 sedemikian hingga P[Z > zα/2] = α/2. Tabel berikut ini dapat membantu: Tabel Nilai Kritis z
Substitusikan nilai-nilai , zα/2, σ, dan n yang sudah diketahui ke dalam rumus (2). Diperolehlah selang kepercayaan yang diminta.
Contoh 2
Untuk melakukan estimasi terhadap rata-rata banyaknya uang yang dihabiskan per bulan untuk membeli rokok, seseorang melakukan sampling terhadap 16 orang perokok dan dari sampel tersebut diperoleh nilai rata-rata Rp 300 ribu. Jika simpangan baku populasi banyaknya uang yang dihabiskan per bulan untuk membeli rokok adalah Rp 30 ribu dan populasi ini berdistribusi normal, tentukanlah selang kepercayaan 95% bagi rata-rata banyaknya yang dihabiskan per bulan untuk membeli rokok populasi tersebut.
Jawab:
Pada contoh ini, , σ = Rp 30 ribu, n = 16, dan γ = 95% = 0,95. Karena simpangan baku populasi diketahui dan populasi berdistribusi normal, rumus (2) boleh dipergunakan.
Langkah 1
α = 1 – 0,95 = 0,05.
α/2 = 0,05/2 = 0,025
Langkah 2
Dari tabel luas daerah di bawah kurva normal baku diperoleh bahwa P[Z > 1,96] ≈ 0,025 sehingga z0,025 = 1,96. (Atau bisa juga menggunakan tabel berikut: Tabel Nilai Kritis z)
Langkah 3
Substitusikan nilai-nilai yang telah didapat di atas ke dalam rumus (2):
Dari sini diperoleh selang kepercayaan 95%: Rp 285.300 < μ < Rp 314.700.
Jadi, kita 95% yakin bahwa rata-rata banyaknya uang yang dihabiskan per bulan untuk membeli rokok adalah antara Rp 285.300 dan Rp 314.700.
Contoh 3
Untuk melakukan estimasi terhadap rata-rata banyaknya uang yang dihabiskan per bulan untuk membeli rokok, seseorang melakukan sampling terhadap 50 orang perokok dan dari sampel tersebut diperoleh nilai rata-rata Rp 300 ribu. Jika simpangan baku populasi banyaknya uang yang dihabiskan per bulan untuk membeli rokok adalah Rp 30 ribu, tentukanlah selang kepercayaan 95% bagi rata-rata banyaknya yang dihabiskan per bulan untuk membeli rokok populasi tersebut.
Jawab:
Pada contoh ini, , σ = Rp 30 ribu, n = 50, dan γ = 95% = 0,95. Syarat pertama penggunaan rumus (2) dipenuhi, yaitu simpangan baku populasi diketahui. Dalam contoh ini populasi tidak diketahui berdistribusi normal. Namun, karena n ≥ 30, syarat kedua pun dipenuhi, sehingga rumus (2) boleh digunakan.
Langkah 1
α = 1 – 0,95 = 0,05.
α/2 = 0,05/2 = 0,025
Langkah 2
Dari tabel luas daerah di bawah kurva normal baku diperoleh bahwa P[Z > 1,96] ≈ 0,025 sehingga z0,025 = 1,96. (Atau bisa juga menggunakan tabel berikut: Tabel Nilai Kritis z)
Langkah 3
Substitusikan nilai-nilai yang telah didapat di atas ke dalam rumus (2):
Dari sini diperoleh selang kepercayaan 95%: Rp 291.684 < μ < Rp 308.316.
Jadi, kita 95% yakin bahwa rata-rata banyaknya uang yang dihabiskan per bulan untuk membeli rokok adalah antara Rp 291.684 dan Rp 308.316.
Pada Contoh 2, simpangan baku populasi diketahui. Bagaimana apabila yang diketahui adalah simpangan baku sampel dan simpangan baku populasi tidak diketahui? Dalam hal ini rumus (3) dapat digunakan dengan syarat n ≥ 30.
Syarat Penggunaan Rumus (3)
Ukuran sampel tidak kurang dari 30.
Langkah-langkah Penggunaan Rumus (3)
Hitunglah α = 1 – γ dan α/2. γ menyatakan derajat kepercayaan.
Dengan menggunakan tabel luas daerah di bawah kurva normal baku, carilah nilai zα/2 sedemikian hingga P[Z > zα/2] = α/2.
Substitusikan nilai-nilai , zα/2, s, dan n yang sudah diketahui ke dalam rumus (3). Diperolehlah selang kepercayaan yang diminta.
Contoh 4
Untuk menaksir rata-rata populasi lamanya pendengar suatu radio menikmati suatu acara di radio, seseorang melakukan sampling terhadap 100 penggemar acara tersebut dan dari hasil sampling tersebut diperoleh rata-rata 90 menit dengan simpangan baku 10 menit. Tentukan selang kepercayaan 97% bagi rata-rata populasi lamanya mendengar acara tersebut.
Jawab:
Pada contoh ini, , s = 10 menit, n = 100, dan γ = 97% = 0,97. Karena n ≥ 30, rumus (3) boleh digunakan.
Langkah 1
α = 1 – 0,97 = 0,03.
α/2 = 0,03/2 = 0,015
Langkah 2
Dari tabel luas daerah di bawah kurva normal baku diperoleh bahwa P[Z > 2,17] ≈ 0,015 sehingga z0,015 = 2,17.
Langkah 3
Substitusikan nilai-nilai yang telah didapat di atas ke dalam rumus (3):
PENAKSIRAN RATA-RATA POPULASI (2)
Di post saya yang lalu telah diuraikan bahwa ada tiga rumus yang dapat digunakan untuk menaksir rata-rata populasi dengan derajat kepercayaan tertentu:
Pada post ini akan dibahas penggunaan rumus (2) dan (3).
Syarat Penggunaan Rumus (2)
Langkah-langkah Penggunaan Rumus (2)
Contoh 2
Untuk melakukan estimasi terhadap rata-rata banyaknya uang yang dihabiskan per bulan untuk membeli rokok, seseorang melakukan sampling terhadap 16 orang perokok dan dari sampel tersebut diperoleh nilai rata-rata Rp 300 ribu. Jika simpangan baku populasi banyaknya uang yang dihabiskan per bulan untuk membeli rokok adalah Rp 30 ribu dan populasi ini berdistribusi normal, tentukanlah selang kepercayaan 95% bagi rata-rata banyaknya yang dihabiskan per bulan untuk membeli rokok populasi tersebut.
Jawab:
Pada contoh ini,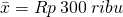
, σ = Rp 30 ribu, n = 16, dan γ = 95% = 0,95. Karena simpangan baku populasi diketahui dan populasi berdistribusi normal, rumus (2) boleh dipergunakan.
Langkah 1
α = 1 – 0,95 = 0,05.
α/2 = 0,05/2 = 0,025
Langkah 2
Dari tabel luas daerah di bawah kurva normal baku diperoleh bahwa P[Z > 1,96] ≈ 0,025 sehingga z0,025 = 1,96. (Atau bisa juga menggunakan tabel berikut: Tabel Nilai Kritis z)
Langkah 3
Substitusikan nilai-nilai yang telah didapat di atas ke dalam rumus (2):
Dari sini diperoleh selang kepercayaan 95%: Rp 285.300 < μ < Rp 314.700.
Jadi, kita 95% yakin bahwa rata-rata banyaknya uang yang dihabiskan per bulan untuk membeli rokok adalah antara Rp 285.300 dan Rp 314.700.
Contoh 3
Untuk melakukan estimasi terhadap rata-rata banyaknya uang yang dihabiskan per bulan untuk membeli rokok, seseorang melakukan sampling terhadap 50 orang perokok dan dari sampel tersebut diperoleh nilai rata-rata Rp 300 ribu. Jika simpangan baku populasi banyaknya uang yang dihabiskan per bulan untuk membeli rokok adalah Rp 30 ribu, tentukanlah selang kepercayaan 95% bagi rata-rata banyaknya yang dihabiskan per bulan untuk membeli rokok populasi tersebut.
Jawab:
Pada contoh ini,
, σ = Rp 30 ribu, n = 50, dan γ = 95% = 0,95. Syarat pertama penggunaan rumus (2) dipenuhi, yaitu simpangan baku populasi diketahui. Dalam contoh ini populasi tidak diketahui berdistribusi normal. Namun, karena n ≥ 30, syarat kedua pun dipenuhi, sehingga rumus (2) boleh digunakan.
Langkah 1
α = 1 – 0,95 = 0,05.
α/2 = 0,05/2 = 0,025
Langkah 2
Dari tabel luas daerah di bawah kurva normal baku diperoleh bahwa P[Z > 1,96] ≈ 0,025 sehingga z0,025 = 1,96. (Atau bisa juga menggunakan tabel berikut: Tabel Nilai Kritis z)
Langkah 3
Substitusikan nilai-nilai yang telah didapat di atas ke dalam rumus (2):
Dari sini diperoleh selang kepercayaan 95%: Rp 291.684 < μ < Rp 308.316.
Jadi, kita 95% yakin bahwa rata-rata banyaknya uang yang dihabiskan per bulan untuk membeli rokok adalah antara Rp 291.684 dan Rp 308.316.
Pada Contoh 2, simpangan baku populasi diketahui. Bagaimana apabila yang diketahui adalah simpangan baku sampel dan simpangan baku populasi tidak diketahui? Dalam hal ini rumus (3) dapat digunakan dengan syarat n ≥ 30.
Syarat Penggunaan Rumus (3)
Ukuran sampel tidak kurang dari 30.
Langkah-langkah Penggunaan Rumus (3)
Contoh 4
Untuk menaksir rata-rata populasi lamanya pendengar suatu radio menikmati suatu acara di radio, seseorang melakukan sampling terhadap 100 penggemar acara tersebut dan dari hasil sampling tersebut diperoleh rata-rata 90 menit dengan simpangan baku 10 menit. Tentukan selang kepercayaan 97% bagi rata-rata populasi lamanya mendengar acara tersebut.
Jawab:
Pada contoh ini,
, s = 10 menit, n = 100, dan γ = 97% = 0,97. Karena n ≥ 30, rumus (3) boleh digunakan.
Langkah 1
α = 1 – 0,97 = 0,03.
α/2 = 0,03/2 = 0,015
Langkah 2
Dari tabel luas daerah di bawah kurva normal baku diperoleh bahwa P[Z > 2,17] ≈ 0,015 sehingga z0,015 = 2,17.
Langkah 3
Substitusikan nilai-nilai yang telah didapat di atas ke dalam rumus (3):
Dari sini diperoleh selang kepercayaan 97%: 87,83 menit < μ < 92,17 menit.
Jadi, kita 97% yakin bahwa rata-rata lamanya mendengarkan acara di radio tersebut berada dalam kisaran antara 87,83 menit dan 92,17 menit.
LATIHAN SOAL
Latihan Penaksiran Parameter
File presentasi: penaksiran rata-rata
Bagikan ini:
Most visitors also read :
DEKOMPOSISI NILAI SINGULAR (SINGULAR VALUE DECOMPOSITION)
MAXIMUM LIKELIHOOD ESTIMATOR
JARAK STATISTIKAL
SOAL DAN PEMBAHASAN ANALISIS KOMPONEN UTAMA