KEJADIAN SALING LEPAS vs TIDAK SALING LEPAS

Dalam sebuah eksprerimen, kadang-kadang kita temui ada kejadian-kejadian yang tidak mungkin terjadi bersama (bersamaan waktu). Misalnya, pada pelemparan sebuah dadu sebanyak satu kali, tidak mungkin sisi bermata dadu 4 dan sisi bermata dadu 5 muncul bersamaan. Pada pengambilan secara acak satu buah kartu dari satu set kartu bridge, tidak mungkin terambil kartu Queen dan kartu Jack secara bersamaan. Pada pengambilan secara acak satu buah bendera dari sekumpulan bendera berbagai negara, tidak mungkin terambil bendera Indonesia dan bendera Singapura secara bersamaan. Kejadian-kejadian semacam ini dinamakan kejadian yang saling lepas (mutually exclusive). Jika A dan B tidak mungkin terjadi kedua-duanya sekaligus (bersamaan waktu), A dan B dikatakan saling lepas.
Lain halnya dengan kejadian-kejadian pada contoh berikut. Pada pengambilan satu buah kartu secara acak dari satu set kartu bridge, mungkin saja terambil kartu Queen sekaligus kartu dengan buah berwarna merah. Pada pelemparan sebuah dadu, mungkin saja terjadi muncul sisi dengan banyaknya mata dadu ganjil sekaligus lebih dari 3. Pada pengambilan secara acak satu buah bendera dari sekumpulan bendera setiap negara di dunia, mungkin saja terambil bendera negara ASEAN sekaligus bendera negara bekas jajahan Inggris. Kejadian-kejadian semacam ini, yang mungkin terjadi bersamaan waktu (sekaligus), dinamakan kejadian yang tidak saling lepas (not mutually exclusive). Jika A dan B mungkin terjadi kedua-duanya sekaligus (bersamaan waktu), A dan B dikatakan tidak saling lepas.
Secara umum, jika A dan B masing-masing kejadian maka peluang terjadinya A atau B adalah
P(A∪B) = P(A) + P(B) – P(A∩B) ………………………………………………………………… (*)
dengan:
P(A) = peluang terjadinya A
P(B) = peluang terjadinya B
P(A∩B) = peluang terjadinya A dan B
Namun, jika A dan B saling lepas maka A dan B tidak mungkin keduanya sekaligus terjadi sehingga P(A∩B) = 0 dan selanjutnya, peluang terjadinya A atau B adalah
P(A∪B) = P(A) + P(B)
Contoh 1
Dua puluh buah kartu dengan ukuran dan bahan yang identik diberikan nomor 1 sampai dengan 20. Dari kumpulan kartu tersebut, diambil sebuah kartu secara acak. Berapakah peluang terambilnya kartu dengan bilangan yang lebih dari 12 atau bilangan tersebut habis dibagi 3?
Jawab:
Misalkan A = kejadian terambil kartu dengan bilangan lebih dari 12 dan B = kejadian terambil kartu dengan bilangan yang habis dibagi 3. Dalam hal ini, ruang sampelnya adalah S = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20}.
A = {13, 14, 15, 16, 17, 18, 19, 20}
B = {3, 6, 9, 12, 15, 18}.
Selanjutnya, A∩B = {15, 18}.
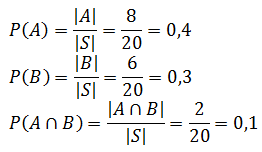
Dengan rumus (*), diperoleh P(A∪B) = 0,4 + 0,3 – 0,1 = 0,6.
Jadi, peluang terambilnya kartu dengan bilangan yang lebih dari 12 atau bilangan tersebut habis dibagi 3 adalah 0,6.
Contoh 2
Dari satu set kartu bridge tanpa Joker, diambil secara acak 1 buah kartu. Berapa peluang terambilnya kartu bergambar diamond atau kartu bergambar wajah?
Jawab:
Misalkan A = kejadian terambil kartu bergambar diamond dan B = kejadian terambil kartu bergambar wajah. Dalam hal ini, ruang sampelnya adalah S = {2♠, 3♠, 4♠, 5♠, 6♠, 7♠, 8♠, 9♠, 10♠, J♠, Q♠, K♠, A♠, 2♣, 3♣, 4♣, 5♣, 6♣, 7♣, 8♣, 9♣, 10♣, J♣, Q♣, K♣, A♣, 2♥, 3♥, 4♥, 5♥, 6♥, 7♥, 8♥, 9♥, 10♥, J♥, Q♥, K♥, A♥, 2♦, 3♦, 4♦, 5♦, 6♦, 7♦, 8♦, 9♦, 10♦, J♦, Q♦, K♦, A♦}.
A = {2♦, 3♦, 4♦, 5♦, 6♦, 7♦, 8♦, 9♦, 10♦, J♦, Q♦, K♦, A♦}
B = {J♠, Q♠, K♠, J♣, Q♣, K♣, J♥, Q♥, K♥, J♦, Q♦, K♦}.
Selanjutnya, A ∩ B = {J♦, Q♦, K♦}.

Dengan rumus (*), diperoleh:
![]()
Jadi, peluang terambilnya kartu bergambar diamond atau kartu bergambar wajah adalah 0,4231.
Pada Contoh 1 dan Contoh 2, pasangan-pasangan kejadian yang diberikan merupakan kejadian-kejadian yang tidak saling lepas. Perhatikan bahwa pada kedua contoh tersebut, P(A∩B) ≠ 0.
Contoh 3
Dari satu set kartu bridge tanpa Joker, diambil secara acak 1 buah kartu. Berapa peluang terambilnya kartu bergambar diamond atau kartu bergambar hati?
Jawab:
Misalkan A = kejadian terambil kartu bergambar diamond dan B = kejadian terambil kartu bergambar hati. Dalam hal ini, ruang sampelnya adalah S = {2♠, 3♠, 4♠, 5♠, 6♠, 7♠, 8♠, 9♠, 10♠, J♠, Q♠, K♠, A♠, 2♣, 3♣, 4♣, 5♣, 6♣, 7♣, 8♣, 9♣, 10♣, J♣, Q♣, K♣, A♣, 2♥, 3♥, 4♥, 5♥, 6♥, 7♥, 8♥, 9♥, 10♥, J♥, Q♥, K♥, A♥, 2♦, 3♦, 4♦, 5♦, 6♦, 7♦, 8♦, 9♦, 10♦, J♦, Q♦, K♦, A♦}.
A = {2♦, 3♦, 4♦, 5♦, 6♦, 7♦, 8♦, 9♦, 10♦, J♦, Q♦, K♦, A♦}
B = {2♥, 3♥, 4♥, 5♥, 6♥, 7♥, 8♥, 9♥, 10♥, J♥, Q♥, K♥}.
Selanjutnya, A ∩ B = { } (himpunan kosong)

Dengan rumus (*), diperoleh:
![]()
Jadi, peluang terambilnya kartu bergambar diamond atau kartu bergambar hati adalah 0,5.
Pada Contoh 3, P(A∩B) = 0. Jadi, pada pengambilan satu buah kartu secara acak dari satu set kartu bridge tersebut, tidak mungkin terambil kartu diamond dan kartu hati secara bersamaan. Ini merupakan contoh kejadian-kejadian yang saling lepas.
Contoh 4
Tiga buah uang logam dilemparkan bersamaan. Berapakah peluang muncul tepat 1 sisi gambar (G) atau tepat 1 sisi angka (A)?
Jawab:
Misalkan A = kejadian muncul tepat 1 sisi G dan B = kejadian muncul tepat 1 sisi A. Ruang sampel pada eksperimen ini adalah S = {AAA, AAG, AGA, GAA, GGA, GAG, AGG, GGG}.
A = {GAA, AGA, AAG}
B = {GGA, GAG, AGG}
A∩B = { } (himpunan kosong)

Dengan rumus (*), diperoleh:
![]()
Jadi, peluang muncul tepat 1 sisi gambar (G) atau tepat 1 sisi angka (A) adalah 0,75.
Pada Contoh 4, P(A∩B) = 0. Ini menunjukkan bahwa kejadian-kejadian tersebut saling lepas, kejadian-kejadian tersebut tidak mungkin terjadi bersamaan. Pada pelemparan tiga uang logam sekaligus, tidak mungkin kemunculan tepat 1 sisi gambar bersamaan dengan kemunculan tepat 1 sisi angka.
Penjelasan secara audiovisual dapat dilihat di link berikut: https://www.youtube.com/watch?v=1DBbdGSLNLY
File pdf terkait tautan youtube di atas: (klik di sini)
Baca juga: mutually exclusive events di edcommstatistics.wordpress.com




Terima kasih atas bantuannya.