Di post saya sebelumnya telah diterangkan bahwa ada tiga statistik yang dapat digunakan untuk melakukan uji hipotesis dua-sampel mengenai rata-rata. Ketiga statistik tersebut adalah sebagai berikut.
Penggunaan (1) telah dibahas pada post sebelumnya. Post ini membahas penggunaan (2).
Kedua sampel diambil dari populasi yang masing-masing berdistribusi normal.
Simpangan baku atau variansi kedua populasi diketahui sama besar.
Kedua sampel saling bebas, tidak saling berhubungan.
Contoh 2
Terdapat dua acara serupa yang disiarkan di dua stasiun radio yang berbeda, yaitu stasiun radio A dan stasiun radio B. Terdapat suatu dugaan bahwa pendengar acara tersebut di stasiun radio A lebih lama mengikuti acara tersebut daripada pendengar acara serupa di stasiun radio B. Untuk memeriksa hal ini, diambillah secara acak 10 orang pendengar acara tersebut di stasiun radio A dan diperoleh rata-rata lamanya mendengarkan acara tersebut adalah 45 menit dengan simpangan baku 6 menit. Dari populasi pendengar acara tersebut di stasiun radio B diambil pula sampel acak berukuran 15 dan diperoleh rata-rata lamanya mendengarkan acara tersebut adalah 42 menit dengan simpangan baku 3 menit. Apakah sampel yang diambil ini mendukung pernyataan bahwa pendengar acara tersebut di stasiun radio A lebih lama mengikuti acara tersebut daripada pendengar acara serupa di stasiun radio B? Gunakan taraf nyata 0,05. Anggaplah kedua populasi berdistribusi normal dengan simpangan baku yang sama.
Bandingkan dengan soal pada Contoh 1 pada post saya sebelumnya. Pada Contoh 1, yang diketahui adalah masing-masing simpangan baku populasi. Pada Contoh 2, yang diketahui adalah simpangan baku masing-masing sampel! Pada Contoh 2, simpangan baku masing-masing populasi tidak diketahui, tetapi diketahui bahwa kedua populasi tersebut memiliki simpangan baku yang sama besar.
Jawaban Contoh 2
Misalkan
Rata-rata lamanya mendengarkan acara tersebut di stasiun radio A adalah μA.
Rata-rata lamanya mendengarkan acara tersebut di stasiun radio B adalah μB.
Pada contoh ini, , nA = 10, sA = 6 menit, , nB = 15, sB = 3 menit. α = 0,05.
Langkah 1 dan 2
H0: μA = μB
H1: μA > μB
Pasangan hipotesis tersebut dapat ditulis kembali sebagai berikut.
H0: μA – μB = 0
H1: μA – μB > 0
Langkah 3
α = 0,05
Langkah 4
Pada contoh ini, kedua simpangan baku sampel diketahui, masing-masing populasi berdistribusi normal, sampel-sampel ini saling bebas, dan kedua populasi memiliki simpangan baku yang sama. Jadi rumus (2) dapat digunakan. Daerah kritisnya adalah t > t0,05;23. (23 = df = 10+15-2, lihat catatan di bawah rumus (2).) Dari tabel nilai kritis t, diperoleh daerah kritis t > 1,714 (lihat gambar di bawah.)
Langkah 5
Substitusikan nilai-nilai yang telah diketahui ke dalam (2), diperoleh:
Langkah 6
Karena statistik uji pada Langkah 5 jatuh di daerah penerimaan, kita tak dapat menolak H0. Jadi, sampel tersebut tidak mendukung pernyataan bahwa pendengar acara tersebut di stasiun radio A lebih lama mengikuti acara tersebut daripada pendengar acara serupa di stasiun radio B.Bukti yang telah diperoleh tidak cukup untuk menyimpulkan bahwa pendengar acara tersebut di stasiun radio A lebih lama mengikuti acara tersebut daripada pendengar acara serupa di stasiun radio B.
UJI HIPOTESIS DUA-SAMPEL (2)
Di post saya sebelumnya telah diterangkan bahwa ada tiga statistik yang dapat digunakan untuk melakukan uji hipotesis dua-sampel mengenai rata-rata. Ketiga statistik tersebut adalah sebagai berikut.
Penggunaan (1) telah dibahas pada post sebelumnya. Post ini membahas penggunaan (2).
Rumus (2)
Catatan: n1 + n2 – 2 = df (degree of freedom, derajat kebebasan)
Syarat penggunaan:
Contoh 2
Terdapat dua acara serupa yang disiarkan di dua stasiun radio yang berbeda, yaitu stasiun radio A dan stasiun radio B. Terdapat suatu dugaan bahwa pendengar acara tersebut di stasiun radio A lebih lama mengikuti acara tersebut daripada pendengar acara serupa di stasiun radio B. Untuk memeriksa hal ini, diambillah secara acak 10 orang pendengar acara tersebut di stasiun radio A dan diperoleh rata-rata lamanya mendengarkan acara tersebut adalah 45 menit dengan simpangan baku 6 menit. Dari populasi pendengar acara tersebut di stasiun radio B diambil pula sampel acak berukuran 15 dan diperoleh rata-rata lamanya mendengarkan acara tersebut adalah 42 menit dengan simpangan baku 3 menit. Apakah sampel yang diambil ini mendukung pernyataan bahwa pendengar acara tersebut di stasiun radio A lebih lama mengikuti acara tersebut daripada pendengar acara serupa di stasiun radio B? Gunakan taraf nyata 0,05. Anggaplah kedua populasi berdistribusi normal dengan simpangan baku yang sama.
Bandingkan dengan soal pada Contoh 1 pada post saya sebelumnya. Pada Contoh 1, yang diketahui adalah masing-masing simpangan baku populasi. Pada Contoh 2, yang diketahui adalah simpangan baku masing-masing sampel! Pada Contoh 2, simpangan baku masing-masing populasi tidak diketahui, tetapi diketahui bahwa kedua populasi tersebut memiliki simpangan baku yang sama besar.
Jawaban Contoh 2
Misalkan
Rata-rata lamanya mendengarkan acara tersebut di stasiun radio A adalah μA.
Rata-rata lamanya mendengarkan acara tersebut di stasiun radio B adalah μB.
Pada contoh ini, , nA = 10, sA = 6 menit,
, nA = 10, sA = 6 menit, 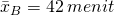 , nB = 15, sB = 3 menit. α = 0,05.
, nB = 15, sB = 3 menit. α = 0,05.
Langkah 1 dan 2
H0: μA = μB
H1: μA > μB
Pasangan hipotesis tersebut dapat ditulis kembali sebagai berikut.
H0: μA – μB = 0
H1: μA – μB > 0
Langkah 3
α = 0,05
Langkah 4
Pada contoh ini, kedua simpangan baku sampel diketahui, masing-masing populasi berdistribusi normal, sampel-sampel ini saling bebas, dan kedua populasi memiliki simpangan baku yang sama. Jadi rumus (2) dapat digunakan. Daerah kritisnya adalah t > t0,05;23. (23 = df = 10+15-2, lihat catatan di bawah rumus (2).) Dari tabel nilai kritis t, diperoleh daerah kritis t > 1,714 (lihat gambar di bawah.)
Langkah 5
Substitusikan nilai-nilai yang telah diketahui ke dalam (2), diperoleh:
Langkah 6
Karena statistik uji pada Langkah 5 jatuh di daerah penerimaan, kita tak dapat menolak H0. Jadi, sampel tersebut tidak mendukung pernyataan bahwa pendengar acara tersebut di stasiun radio A lebih lama mengikuti acara tersebut daripada pendengar acara serupa di stasiun radio B. Bukti yang telah diperoleh tidak cukup untuk menyimpulkan bahwa pendengar acara tersebut di stasiun radio A lebih lama mengikuti acara tersebut daripada pendengar acara serupa di stasiun radio B.
(bersambung)
Bagikan ini:
Most visitors also read :
DEKOMPOSISI NILAI SINGULAR (SINGULAR VALUE DECOMPOSITION)
MAXIMUM LIKELIHOOD ESTIMATOR
JARAK STATISTIKAL
SOAL DAN PEMBAHASAN ANALISIS KOMPONEN UTAMA