UJI HIPOTESIS DUA-SAMPEL (1)

November 14th, 2016

Di post saya yang lalu, telah diperkenalkan konsep dasar uji hipotesis dan bagaimana uji hipotesis dalam statistika dilakukan. Di salah satu contoh yang diberikan, kita menguji apakah rata-rata waktu menunggu di suatu restoran cepat saji lebih dari 5 menit. Pada contoh itu, kita melakukan pengujian terhadap rata-rata satu buah populasi, yaitu populasi lamanya waktu menunggu di suatu restoran. Sekarang, bagaimana kita membandingkan rata-rata dua buah populasi? Sebagai contoh, kita memiliki suatu hipotesis: menunggu makanan siap di Rumah Makan “Enak” lebih lama dari Rumah Makan “Lezat”. Dalam “bahasa statistika”, ini sama dengan mengatakan bahwa rata-rata lamanya waktu menunggu di Rumah Makan “Enak” lebih besar dari rata-rata lamanya waktu menunggu di Rumah Makan “Lezat”. Pada contoh yang melibatkan dua rumah makan ini ada dua populasi yang dilibatkan, yaitu populasi lama waktu tunggu di Rumah Makan “Enak” dan populasi lama waktu tunggu di Rumah Makan “Lezat”. Dalam ilmu statistika, permasalahan ini merupakan suatu topik dalam Uji Hipotesis Dua-Sampel (Two-Sample Tests of Hypotheses).

 

Post ini membahas uji hipotesis dua-sampel rata-rata. Uji ini pun terdiri dari dua macam, yaitu a) uji rata-rata dua-sampel yang saling bebas (independent) dan b) uji rata-rata dua-sampel yang tidak saling bebas (seringkali dinamakan observasi berpasangan). Pembahasan pada post ini dibatasi pada uji rata-rata dua-sampel yang saling bebas.

 

Untuk uji hipotesis dua-sampel rata-rata ini ada tiga macam statistik yang dapat digunakan, yaitu:

set_rumus_uh_2s

Mengenai rumus mana yang digunakan, tergantung dari situasi yang dihadapi. Pada post kali ini hanya akan dibahas penggunaan rumus (1). Penggunaan kedua rumus lainnya akan dibahas pada post saya yang lain.

 

Pada prinsipnya, langkah-langkah pengujian hipotesis dua-sampel sama dengan pengujian hipotesis satu-sampel sebagaimana yang telah dibahas pada post saya sebelumnya. Yang berbeda hanyalah statistik yang digunakan (Langkah 4). Langkah-langkah selengkapnya adalah sebagai berikut.

  1. Tentukan hipotesis nol H0: θ = θ0.
  2. Tentukan hipotesis tandingan yang cocok, yaitu salah satu dari θ ≠ θ0, θ < θ0, atau θ > θ0.
  3. Tentukan taraf nyata (α) yang dikehendaki.
  4. Tentukan statistik uji yang sesuai dan tentukan pula daerah kritisnya.
  5. Hitunglah nilai uji statistik dari data sampel.
  6. Tolak H0­ jika statistik uji pada langkah 5 jatuh dalam daerah kritis. Dalam hal lain, jangan tolak H0 karena tidak cukup bukti untuk menolak H0.

 

 

Rumus (1)

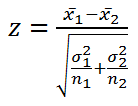
r1_uh_2s

Syarat penggunaan:

  1. Kedua sampel diambil dari populasi yang masing-masing berdistribusi normal.
  2. Simpangan baku atau variansi masing-masing populasi diketahui.
  3. Kedua sampel saling bebas, tidak saling berhubungan.

 

Contoh 1

Terdapat dua acara serupa yang disiarkan di dua stasiun radio yang berbeda, yaitu stasiun radio A dan stasiun radio B. Terdapat suatu dugaan bahwa pendengar acara tersebut di stasiun radio A lebih lama mengikuti acara tersebut daripada pendengar acara serupa di stasiun radio B. Untuk memeriksa hal ini, diambillah secara acak 15 orang pendengar acara tersebut di stasiun radio A dan diperoleh rata-rata lamanya mendengarkan acara tersebut adalah 45 menit. Dari populasi pendengar acara tersebut di stasiun radio B diambil pula sampel acak berukuran 20 dan diperoleh rata-rata lamanya mendengarkan acara tersebut adalah 42 menit. Jika simpangan baku lamanya mendengarkan acara tersebut di stasiun radio A adalah 6 menit dan di stasiun radio B adalah 3 menit, apakah sampel yang diambil ini mendukung pernyataan bahwa pendengar acara tersebut di stasiun radio A lebih lama mengikuti acara tersebut daripada pendengar acara serupa di stasiun radio B? Gunakan taraf nyata 0,05. Anggap kedua populasi berdistribusi normal.

 

Jawab:

Misalkan

Rata-rata lamanya mendengarkan acara tersebut di stasiun radio A adalah μA.

Rata-rata lamanya mendengarkan acara tersebut di stasiun radio B adalah μB.

Pada contoh ini, {\bar{x}}_A = 45 \: menit, n_A = 15, {\sigma}_A = 6 \: menit, {\bar{x}}_B = 42 \: menit, n_B = 20, {\sigma}_B = 3 \: menit. α = 0,05.

 

Langkah 1 dan 2

H0: μA = μB

H1: μA > μB

Pasangan hipotesis tersebut dapat ditulis kembali sebagai berikut.

H0: μA – μB = 0

H1: μA – μB > 0

Langkah 3

α = 0,05

Langkah 4

Pada contoh ini, kedua simpangan baku populasi diketahui, masing-masing populasi berdistribusi normal, dan sampel-sampel ini saling bebas. Jadi rumus (1) dapat digunakan. Daerah kritisnya adalah z > z0,05. Dari tabel nilai kritis z, diperoleh daerah kritis z > 1,64 (lihat gambar di bawah.)

uh_rata2_2s_contoh_1

 

Langkah 5

Substitusikan nilai-nilai yang telah diketahui ke dalam (1), diperoleh:

z_rata2_2s_contoh_1

Langkah 6

uh_rata2_2s_contoh_1a

Karena statistik uji pada Langkah 5 jatuh di daerah kritis/daerah penolakan, tolak H0. Jadi, sampel tersebut mendukung pernyataan bahwa pendengar acara tersebut di stasiun radio A lebih lama mengikuti acara tersebut daripada pendengar acara serupa di stasiun radio B. Dengan kata lain, rata-rata lamanya mendengarkan acara tersebut di stasiun radio A secara signifikan lebih besar dari rata-rata lamanya mendengarkan acara tersebut di stasiun radio B.

 

(bersambung)



Most visitors also read :



Satu tanggapan untuk “UJI HIPOTESIS DUA-SAMPEL (1)”

  1. eky berkata:
    Desember 28, 2017 pukul 00:20

    Mau nanya. Kapan kita harus pake uji z kapan kita pake uji t? Apakah critical region ditentukan berdasarkan hasil uji tabel bukan uji z atau uji t nya? Atau critical region yg diciptakan oleh uji z dan uji t berbeda?
    Hari ini saya ujian jam 7.30. Smg anda bisa membalas sebelum jam tsb. Terimakasih sebelumnya

    Balas

Tinggalkan Balasan

Alamat email Anda tidak akan dipublikasikan.