Di post terdahulu kita mempelajari bagaimana menguji atau memeriksa adanya hubungan di antara dua buah variabel kategorik/nominal. Post kali ini membahas bagaimana memeriksa adanya hubungan di antara dua buah variabel yang masing-masingnya memiliki tingkat ordinal atau yang lebih tinggi (kuantitatif). Koefisien korelasi yang dapat digunakan untuk tingkat data ini adalah Spearman’s Rho atau Spearman’s Rank-Order Correlation Coefficient, yang dilambangkan dengan . Koefisien ini ditemukan Charles Edward Spearman (1863-1945), seorang ahli psikologi Inggris yang banyak berkontribusi dalam perkembangan ilmu statistika. Ia seorang pelopor analisis faktor, suatu analisis yang banyak digunakan dalam penelitian kuantitatif di lapangan ilmu sosial.
Pengujian hubungan dengan Spearman’s Rho ini merupakan salah satu contoh uji statistik nonparametrik. Jadi, tidak diperlukan asumsi bahwa populasi asal sampel memiliki distribusi peluang teoretis tertentu. Karena tidak adanya asumsi tersebut, Spearman’s Rho biasa dijadikan alternatif apabila ternyata populasi asal sampel tidak berdistribusi normal. (Apabila populasi asal masing-masing sampel berdistribusi normal, ada alternatif pengujian hubungan dengan Pearson’s Product-Moment Correlation.) Dalam korelasi Spearman, yang dihitung koefisien korelasinya adalah antara peringkat (rank) nilai-nilai pada variabel pertama dan rank nilai-nilai pada variabel kedua. (Lihat penjelasannya di bawah.)
Nilai Spearman’s Rho hasil sampling adalah . Dalam rumus tersebut, n adalah ukuran sampel, dan untuk i = 1, 2, …, n, adalah selisih antara peringkat sampel ke-i pada variabel pertama dengan peringkat sampel ke-i pada variabel kedua. Sebagai contoh, misalkan terdapat dua buah variabel X dan Y, dan hasil sampling menunjukkan nilai-nilai X dan Y sebagai berikut.
Tabel 1
Pertama-tama, kita memberikan peringkat bagi setiap nilai pada masing-masing variabel. Sebagai contoh, untuk variabel X, kita berikan peringkat (rank) 1 untuk data terkecil dalam X, yaitu 15. Bilangan yang lebih besar berikutnya setelah 15 adalah 19, sehingga terhadap 19 kita berikan peringkat 2, dan seterusnya, hingga nilai terbesar X adalah 50, yang kepadanya kita berikan peringkat 10. Lakukan hal serupa untuk nilai-nilai variabel Y. Dengan demikian, hasil pemeringkatan tersebut dapat dilihat di tabel berikut.
Tabel 2
Pada Tabel 2, kolom rank(X) berisikan peringkat-peringkat yang diberikan kepada nilai-nilai variabel X dan rank(Y) berisikan peringkat-peringkat yang diberikan kepada nilai-nilai variabel Y. Kemudian tambahkan dua kolom lagi, yaitu kolom di yang berisikan selisih antara rank(X) dan rank(Y) dan kolom di2. Lihat Tabel 3.
Tabel 3
Untuk contoh ini, nilai Spearman’s Rho adalah:
.
Berikut hasil pengolahan data di atas dengan SPSS.
Tabel 4
Tabel tersebut menunjukkan nilai koefisien korelasi Spearman hasil sampling sebesar 0,164, sesuai dengan perhitungan di atas. Dengan hanya melihat nilai ini, kita belum dapat menjawab apakah terdapat hubungan di antara X dan Y. Untuk menyimpulkan apakah terdapat hubungan di antara keduanya, kita perlu melakukan uji hipotesis mengenai nilai ρs. Tentang ini akan dibahas kemudian dalam artikel ini.
Berikut merupakan hal-hal penting yang berkenaan dengan uji korelasi menggunakan Spearman’s Rho.
Range nilai Spearman’s Rho adalah antara -1 dan 1. Nilai ρs yang kecil (mendekati nol) menandakan hubungan yang lemah. Nilai ρs yang mendekati 1 atau -1 menandakan hubungan yang kuat.
Jika ρs > 0, kedua variabel bergerak searah. Ini berarti bahwa: nilai X bertambah seiring pertambahan nilai Y, dan nilai X berkurang seiring berkurangnya nilai Y.
Jika ρs < 0, kedua variabel bergerak berlawanan arah. Ini berarti bahwa: nilai X bertambah seiring berkurangnya nilai Y, dan nilai X berkurang seiring bertambahnya nilai Y.
Jika ρs = 0 maka tidak dapat disimpulkan bahwa kedua variabel tidak berhubungan.
Kondisi ρs≠ 0 tidak secara otomatis mengizinkan kita untuk menyimpulkan bahwa ada hubungan sebab-akibat di antara keduanya, walaupun hasil ujinya signifikan. Hubungan sebab-akibat tidak dapat disimpulkan dari hanya mengandalkan uji signifikansi statistik.
SIGNIFIKANSI UJI DENGAN SPEARMAN’S RHO
Untuk menguji apakah terdapat hubungan di antara dua buah variabel dengan tingkat data ordinal atau lebih tinggi, terdapat tiga kemungkinan hipotesis alternatif (H1).
Kemungkinan I: ρs ≠ 0
Kemungkinan II: ρs > 0 (uji satu ekor, uji ekor kanan)
Kemungkinan III: ρs < 0 (uji satu ekor, uji ekor kiri)
Hipotesis nol dalam uji ini adalah: “Tidak ada hubungan antara kedua variabel”.
Dalam memutuskan apakah hipotesis nol harus ditolak atau tidak, kita dapat menggunakan tabel nilai kritis koefisien korelasi Spearman (klik di sini), atau, untuk ukuran sampel n > 100, menggunakan statistik t berikut: dengan derajat kebebasan ν = n-2.
Tentang penggunaan tabel nilai kritis
Nilai kritis yang digunakan tergantung dari ukuran sampel (n) dan taraf nyata (α). Dalam tabel tersebut, judul-judul baris menunjukkan ukuran sampel dan judul-judul kolom menunjukkan taraf nyata. Jika ujinya bersifat satu ekor (1-tailed) maka judul kolom yang digunakan adalah yang ditandai dengan α(1). Jika ujinya bersifat dua ekor (2-tailed) maka judul kolom yang digunakan adalah yang ditandai dengan α(2). Sebagai contoh, apabila ukuran sampelnya 15 dan ujinya bersifat satu ekor kanan dengan taraf nyata 0,05 maka berdasarkan tabel tersebut, nilai kritis rs-nya adalah sebesar 0,446. Apabila ukuran sampelnya 20 dan ujinya bersifat dua ekor dengan taraf nyata 0,01, maka nilai kritis rs-nya adalah 0,570.
Tabel berikut ini digunakan untuk memutuskan apakah hipotesis nol ditolak.
Tabel 5
Tentang penggunaan statistik t
Tabel nilai kritis korelasi Spearman tidak memberikan nilai kritis apabila ukuran sampel lebih dari 100. Untuk memberikan keputusan mengenai hipotesis nol, kita menggunakan statistik dengan derajat kebebasan ν = n-2. Gunakan tabel berikut untuk mengetahui kriteria penolakan H0.
Tabel 6
Untuk menentukan tkritis uji satu ekor, kita dapat menggunakan tabel nilai kritis t atau menggunakan bantuan perangkat lunak Excel. Untuk mengetahui tkritis dengan Excel, gunakan =ABS(T.INV()). Sebagai contoh, apabila α = 0,05 dan derajat kebebasannya adalah n = 13 maka ketikkan ekspresi berikut di salah satu sel lembar kerja Excel: =ABS(T.INV(0.05;13)) dan Excel akan menampilkan nilai 1,771. Untuk menentukan tkritis uji dua ekor, kita dapat menggunakan tabel nilai kritis t atau dengan mengetikkan =T.INV.2T() di salah satu sel dalam lembar kerja Excel. Sebagai contoh, dalam uji dua ekor, nilai kritis t untuk taraf nyata 0,05 dan derajat kebebasan 18 dapat diperoleh dengan mengetikkan =T.INV.2T(0.05;18) dan Excel akan menampilkan nilai 2,101.
Contoh Kasus
Contoh penelitian di bidang komunikasi yang menggunakan koefisien korelasi Spearman adalah penelitian oleh Adeyeye et. al. (2019) yang berjudul “Data on New Media Use for Agricultural Training and Research at Agricultural Services and Training Centre”. Untuk mendapatkan artikel tersebut, klik di sini. Adeyeye berhipotesis bahwa ada hubungan antara penggunaan internet sebagai sumber materi pelatihan petani dengan penggunaan new media dalam melatih petani. Untuk memeriksa hipotesis itu, para peneliti tersebut menggunakan 47 sampel. Berikut ini adalah uji hipotesis yang dilakukan.
Langkah 1 (Menyusun hipotesis)
H0: Tak ada hubungan antara penggunaan internet sebagai sumber materi pelatihan petani dengan penggunaan new media dalam melatih petani.
H1: ρs ≠ 0 [Ada hubungan antara penggunaan internet sebagai sumber materi pelatihan petani dengan penggunaan new media dalam melatih petani.]
Langkah 2 (Menetapkan taraf nyata)
α = 0,05
Langkah 3 (Menentukan statistik uji dan daerah penolakan)
Statistik yang digunakan adalah . Untuk menentukan daerah penolakan, kita menggunakan tabel nilai kritis koefisien korelasi Spearman dan dari tabel tersebut kita mendapatkan nilai kritis 0,288. Dengan menggunakan Tabel 5, kita mendapatkan kriteria penolakan H0 sebagai berikut: Tolak H0 apabila rs < -0,288 atau rs > 0,288.
Langkah 4 (Menghitung nilai statistik uji hasil sampling)
File data hasil sampling dalam format .sav dapat diunduh dari tautan berikut: (klik di sini). Dalam file tersebut terdapat dua buah variabel, yaitu internet dan newmedia. Variabel internet menyatakan penggunaan internet sebagai sumber materi pelatihan petani dan variabel newmedia menyatakan penggunaan new media dalam melatih petani. Perangkat lunak SPSS Versi 21 memberikan hasil sebagai berikut.
Tabel 7
Dari tabel di atas diperoleh nilai rs = -0,087. Berdasarkan kriteria penolakan H0 pada langkah sebelumnya, nilai rs yang didapat tidak memenuhi kriteria penolakan. Jadi, kita tak boleh menolak H0.
Langkah 5 (Penyimpulan)
Tidak ada hubungan signifikan antara penggunaan internet sebagai sumber materi pelatihan petani dengan penggunaan new media dalam melatih petani.
SOAL 1
Seorang peneliti berhipotesis bahwa ada hubungan antara nilai akhir mata kuliah Statistika dengan nilai skripsi. Untuk itu dilakukanlan sampling terhadap 10 lulusan, dan hasilnya diringkaskan pada tabel berikut.
Pada taraf nyata 0,05, apakah dapat disimpulkan adanya hubungan tersebut?
SOAL 2
Apakah suami dan istri menyukai acara TV yang sama? Sebuah studi terbaru oleh Nielsen Media Research meminta pasangan muda yang sudah menikah untuk memberi peringkat acara dari yang terbaik hingga yang terburuk. Peringkat 1 menunjukkan acara yang paling disukai dan peringkat 14 menunjukkan acara yang paling tidak disukai. Berikut ini adalah hasil untuk satu pasangan yang sudah menikah.
Pada taraf nyata 0,05, apakah cukup beralasan untuk menyimpulkan ada hubungan positif antara kedua peringkat tersebut? Sumber: Lind, D. A., Marchal, W. G., & Wathen, S. A. (2012). Statistical techniques in business & economics (15th ed.). McGraw-Hill Irwin.
KOEFISIEN KORELASI SPEARMAN’S RHO
Di post terdahulu kita mempelajari bagaimana menguji atau memeriksa adanya hubungan di antara dua buah variabel kategorik/nominal. Post kali ini membahas bagaimana memeriksa adanya hubungan di antara dua buah variabel yang masing-masingnya memiliki tingkat ordinal atau yang lebih tinggi (kuantitatif). Koefisien korelasi yang dapat digunakan untuk tingkat data ini adalah Spearman’s Rho atau Spearman’s Rank-Order Correlation Coefficient, yang dilambangkan dengan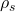
. Koefisien ini ditemukan Charles Edward Spearman (1863-1945), seorang ahli psikologi Inggris yang banyak berkontribusi dalam perkembangan ilmu statistika. Ia seorang pelopor analisis faktor, suatu analisis yang banyak digunakan dalam penelitian kuantitatif di lapangan ilmu sosial.
Pengujian hubungan dengan Spearman’s Rho ini merupakan salah satu contoh uji statistik nonparametrik. Jadi, tidak diperlukan asumsi bahwa populasi asal sampel memiliki distribusi peluang teoretis tertentu. Karena tidak adanya asumsi tersebut, Spearman’s Rho biasa dijadikan alternatif apabila ternyata populasi asal sampel tidak berdistribusi normal. (Apabila populasi asal masing-masing sampel berdistribusi normal, ada alternatif pengujian hubungan dengan Pearson’s Product-Moment Correlation.) Dalam korelasi Spearman, yang dihitung koefisien korelasinya adalah antara peringkat (rank) nilai-nilai pada variabel pertama dan rank nilai-nilai pada variabel kedua. (Lihat penjelasannya di bawah.)
Nilai Spearman’s Rho hasil sampling adalah
. Dalam rumus tersebut, n adalah ukuran sampel, dan untuk i = 1, 2, …, n, 
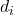adalah selisih antara peringkat sampel ke-i pada variabel pertama dengan peringkat sampel ke-i pada variabel kedua. Sebagai contoh, misalkan terdapat dua buah variabel X dan Y, dan hasil sampling menunjukkan nilai-nilai X dan Y sebagai berikut.
Tabel 1
Pertama-tama, kita memberikan peringkat bagi setiap nilai pada masing-masing variabel. Sebagai contoh, untuk variabel X, kita berikan peringkat (rank) 1 untuk data terkecil dalam X, yaitu 15. Bilangan yang lebih besar berikutnya setelah 15 adalah 19, sehingga terhadap 19 kita berikan peringkat 2, dan seterusnya, hingga nilai terbesar X adalah 50, yang kepadanya kita berikan peringkat 10. Lakukan hal serupa untuk nilai-nilai variabel Y. Dengan demikian, hasil pemeringkatan tersebut dapat dilihat di tabel berikut.
Tabel 2
Pada Tabel 2, kolom rank(X) berisikan peringkat-peringkat yang diberikan kepada nilai-nilai variabel X dan rank(Y) berisikan peringkat-peringkat yang diberikan kepada nilai-nilai variabel Y. Kemudian tambahkan dua kolom lagi, yaitu kolom di yang berisikan selisih antara rank(X) dan rank(Y) dan kolom di2. Lihat Tabel 3.
Tabel 3
Untuk contoh ini, nilai Spearman’s Rho adalah:
Berikut hasil pengolahan data di atas dengan SPSS.
Tabel 4
Tabel tersebut menunjukkan nilai koefisien korelasi Spearman hasil sampling sebesar 0,164, sesuai dengan perhitungan di atas. Dengan hanya melihat nilai ini, kita belum dapat menjawab apakah terdapat hubungan di antara X dan Y. Untuk menyimpulkan apakah terdapat hubungan di antara keduanya, kita perlu melakukan uji hipotesis mengenai nilai ρs. Tentang ini akan dibahas kemudian dalam artikel ini.
Berikut merupakan hal-hal penting yang berkenaan dengan uji korelasi menggunakan Spearman’s Rho.
SIGNIFIKANSI UJI DENGAN SPEARMAN’S RHO
Untuk menguji apakah terdapat hubungan di antara dua buah variabel dengan tingkat data ordinal atau lebih tinggi, terdapat tiga kemungkinan hipotesis alternatif (H1).
Kemungkinan I: ρs ≠ 0
Kemungkinan II: ρs > 0 (uji satu ekor, uji ekor kanan)
Kemungkinan III: ρs < 0 (uji satu ekor, uji ekor kiri)
Hipotesis nol dalam uji ini adalah: “Tidak ada hubungan antara kedua variabel”.
Dalam memutuskan apakah hipotesis nol harus ditolak atau tidak, kita dapat menggunakan tabel nilai kritis koefisien korelasi Spearman (klik di sini), atau, untuk ukuran sampel n > 100, menggunakan statistik t berikut: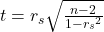
dengan derajat kebebasan ν = n-2.
Tentang penggunaan tabel nilai kritis
Nilai kritis yang digunakan tergantung dari ukuran sampel (n) dan taraf nyata (α). Dalam tabel tersebut, judul-judul baris menunjukkan ukuran sampel dan judul-judul kolom menunjukkan taraf nyata. Jika ujinya bersifat satu ekor (1-tailed) maka judul kolom yang digunakan adalah yang ditandai dengan α(1). Jika ujinya bersifat dua ekor (2-tailed) maka judul kolom yang digunakan adalah yang ditandai dengan α(2). Sebagai contoh, apabila ukuran sampelnya 15 dan ujinya bersifat satu ekor kanan dengan taraf nyata 0,05 maka berdasarkan tabel tersebut, nilai kritis rs-nya adalah sebesar 0,446. Apabila ukuran sampelnya 20 dan ujinya bersifat dua ekor dengan taraf nyata 0,01, maka nilai kritis rs-nya adalah 0,570.
Tabel berikut ini digunakan untuk memutuskan apakah hipotesis nol ditolak.
Tabel 5
Tentang penggunaan statistik t
Tabel nilai kritis korelasi Spearman tidak memberikan nilai kritis apabila ukuran sampel lebih dari 100. Untuk memberikan keputusan mengenai hipotesis nol, kita menggunakan statistik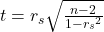
dengan derajat kebebasan ν = n-2. Gunakan tabel berikut untuk mengetahui kriteria penolakan H0.
Tabel 6
Untuk menentukan tkritis uji satu ekor, kita dapat menggunakan tabel nilai kritis t atau menggunakan bantuan perangkat lunak Excel. Untuk mengetahui tkritis dengan Excel, gunakan =ABS(T.INV()). Sebagai contoh, apabila α = 0,05 dan derajat kebebasannya adalah n = 13 maka ketikkan ekspresi berikut di salah satu sel lembar kerja Excel: =ABS(T.INV(0.05;13)) dan Excel akan menampilkan nilai 1,771. Untuk menentukan tkritis uji dua ekor, kita dapat menggunakan tabel nilai kritis t atau dengan mengetikkan =T.INV.2T() di salah satu sel dalam lembar kerja Excel. Sebagai contoh, dalam uji dua ekor, nilai kritis t untuk taraf nyata 0,05 dan derajat kebebasan 18 dapat diperoleh dengan mengetikkan =T.INV.2T(0.05;18) dan Excel akan menampilkan nilai 2,101.
Contoh Kasus
Contoh penelitian di bidang komunikasi yang menggunakan koefisien korelasi Spearman adalah penelitian oleh Adeyeye et. al. (2019) yang berjudul “Data on New Media Use for Agricultural Training and Research at Agricultural Services and Training Centre”. Untuk mendapatkan artikel tersebut, klik di sini. Adeyeye berhipotesis bahwa ada hubungan antara penggunaan internet sebagai sumber materi pelatihan petani dengan penggunaan new media dalam melatih petani. Untuk memeriksa hipotesis itu, para peneliti tersebut menggunakan 47 sampel. Berikut ini adalah uji hipotesis yang dilakukan.
Langkah 1 (Menyusun hipotesis)
H0: Tak ada hubungan antara penggunaan internet sebagai sumber materi pelatihan petani dengan penggunaan new media dalam melatih petani.
H1: ρs ≠ 0 [Ada hubungan antara penggunaan internet sebagai sumber materi pelatihan petani dengan penggunaan new media dalam melatih petani.]
Langkah 2 (Menetapkan taraf nyata)
α = 0,05
Langkah 3 (Menentukan statistik uji dan daerah penolakan)
Statistik yang digunakan adalah
. Untuk menentukan daerah penolakan, kita menggunakan tabel nilai kritis koefisien korelasi Spearman dan dari tabel tersebut kita mendapatkan nilai kritis 0,288. Dengan menggunakan Tabel 5, kita mendapatkan kriteria penolakan H0 sebagai berikut: Tolak H0 apabila rs < -0,288 atau rs > 0,288.
Langkah 4 (Menghitung nilai statistik uji hasil sampling)
File data hasil sampling dalam format .sav dapat diunduh dari tautan berikut: (klik di sini). Dalam file tersebut terdapat dua buah variabel, yaitu internet dan newmedia. Variabel internet menyatakan penggunaan internet sebagai sumber materi pelatihan petani dan variabel newmedia menyatakan penggunaan new media dalam melatih petani. Perangkat lunak SPSS Versi 21 memberikan hasil sebagai berikut.
Tabel 7
Dari tabel di atas diperoleh nilai rs = -0,087. Berdasarkan kriteria penolakan H0 pada langkah sebelumnya, nilai rs yang didapat tidak memenuhi kriteria penolakan. Jadi, kita tak boleh menolak H0.
Langkah 5 (Penyimpulan)
Tidak ada hubungan signifikan antara penggunaan internet sebagai sumber materi pelatihan petani dengan penggunaan new media dalam melatih petani.
SOAL 1
Seorang peneliti berhipotesis bahwa ada hubungan antara nilai akhir mata kuliah Statistika dengan nilai skripsi. Untuk itu dilakukanlan sampling terhadap 10 lulusan, dan hasilnya diringkaskan pada tabel berikut.
Pada taraf nyata 0,05, apakah dapat disimpulkan adanya hubungan tersebut?
SOAL 2
Apakah suami dan istri menyukai acara TV yang sama? Sebuah studi terbaru oleh Nielsen Media Research meminta pasangan muda yang sudah menikah untuk memberi peringkat acara dari yang terbaik hingga yang terburuk. Peringkat 1 menunjukkan acara yang paling disukai dan peringkat 14 menunjukkan acara yang paling tidak disukai. Berikut ini adalah hasil untuk satu pasangan yang sudah menikah.
Pada taraf nyata 0,05, apakah cukup beralasan untuk menyimpulkan ada hubungan positif antara kedua peringkat tersebut? Sumber: Lind, D. A., Marchal, W. G., & Wathen, S. A. (2012). Statistical techniques in business & economics (15th ed.). McGraw-Hill Irwin.
Bagikan ini:
Most visitors also read :
KOEFISIEN KORELASI CRAMER’S V
BEBERAPA CONTOH PELAKSANAAN UJI NORMALITAS
BERKENALAN DENGAN UJI NORMALITAS
VARIABEL ACAK DALAM AKTIVITAS LOGISTIK