Model persediaan (inventory) probabilistik sederhana merupakan suatu perkembangan lebih lanjut dari model Economic Order Quantity yang dipelopori oleh Harris, dengan ciri bahwa permintaan terhadap produk bersifat probabilistik. Dengan tidak menentunya permintaan, mungkin terjadi kekurangan persediaan barang dalam masa ancang-ancang (lead time). Dalam literatur-literatur yang relevan salah satu materi yang menjadi perhatian adalah ekspektasi banyaknya kekurangan persediaan selama waktu ancang-ancang tersebut. Besarnya rata-rata kekurangan ini dibahas juga dalam sebuah buku berjudul Sistem Inventori yang ditulis oleh Senator Nur Bahagia, namun ternyata terdapat kesalahan di dalamnya. Artikel ini dibuat untuk memperbaiki kesalahan tersebut. Dua pendekatan yang telah dilakukan untuk menurunkan rumus ekspektasi shortage tersebut memberikan kesimpulan yang konsisten, yaitu bahwa terdapat kesalahan fatal dalam buku tersebut.
PENDAHULUAN
Salah satu kajian dalam bidang logistik adalah model-model persediaan, yang menurut Erlenkotter dipelopori pertama kali oleh Harris dengan model persediaannya Economic Order Quantity (EOQ) pada tahun 1913. Salah satu asumsi model ini adalah bahwa permintaan bersifat konstan, yang dalam praktik sangat jarang dijumpai. Perkembangan lebih lanjut dapat dilihat dalam Hadley dan Whitin [2], yang banyak mengurai berbagai model persediaan, termasuk model-model persediaan dengan pola permintaan yang bersifat stokastik.
Karya Hadley dan Whitin tersebut telah dijadikan rujukan oleh Bahagia [1] dalam membahas model probabilistik sederhana. Buku karangan Bahagia itu pun sering dijadikan rujukan dalam penelitian-penelitian di bidang persediaan, seperti dapat ditemukan dalam Setiadi dan Raihan [4], Lati dan Aktavia [3], dan Syamil et. al. [5]. Yang menjadi masalah adalah bahwa terdapat rumus yang salah yang ditulis Bahagia [1], yaitu rumus ekspektasi banyaknya kekurangan persediaan (shortage) pada persamaan (7-2) di halaman 136 buku tersebut. Mengingat buku tersebut banyak dijadikan rujukan dalam penelitian-penelitian di bidang persediaan, perlu dilakukan pembetulan terhadap kesalahan tersebut. Urgensi tersebutlah yang melatarbelakangi disusunnya artikel ini.
ASUMSI DAN METODE PENELITIAN
Asumsi yang digunakan dalam penelitian ini adalah: 1) selang waktu antara barang dipesan dan barang tiba, dinamakan lead time, bersifat konstan, 2) permintaan selama lead time berdistribusi normal dengan rata-rata DL dan simpangan baku SL, 3) pemesanan kembali (reorder) dilakukan pada saat tingkat persediaan mencapai r, dan 4) peluang terjadinya kekurangan persediaan selama lead time diketahui sebesar α. Berdasar pada asumsi-asumsi tersebut, penelitian ini akan menjawab berapakah ekspektasi banyaknya kekurangan persediaan selama lead time.
Penelitian ini dilakukan dengan beberapa tahap. Di tahap awal, penurunan rumus ekspektasi banyaknya kekurangan persediaan selama lead time dilakukan berdasarkan proposisi mengenai ekspektasi tersebut sebagaimana dinyatakan oleh Bahagia [1]. Tahap selanjutnya, penurunan rumus yang sama dilakukan dengan bertitik tolak pada salah satu proposisi dalam Hadley dan Whitin [2] sebagai salah satu literatur yang dirujuk oleh Bahagia [1]. Tahap terakhir yaitu menguji konsistensi hasil-hasil yang diperoleh dari kedua pendekatan tersebut.
HASIL DAN PEMBAHASAN
Menurut Bahagia [1], jika x menyatakan banyaknya permintaan selama lead time, r = reorder point, dan f adalah fungsi densitas peluang banyaknya permintaan selama lead time, maka ekspektasi permintaan yang tidak terpenuhi selama lead time, yang untuk selanjutnya dilambangkan dengan N, dapat dinyatakan sebagai berikut.
…………………………………………………………………………………….. (1)
Berdasarkan asumsi penelitian nomor 2, yaitu bahwa permintaan selama lead time berdistribusi normal dengan rata-rata DL dan simpangan baku SL, diperolehlah f(x) = n(x; DL, SL), dengan n(x; DL, SL) menyatakan fungsi densitas peluang normal dengan rata-rata DL dan simpangan baku SL sehingga (1) dapat dinyatakan sebagai:
………………………………………………………………………… (2)
Untuk menyederhanakan notasi, untuk selanjutnya penulisan DL disederhanakan menjadi μ dan SL disederhanakan menjadi σ. Jadi, (2) dapat dinyatakan sebagai . Selanjutnya, dengan mensubstitusikan ke dalam (2), diperolehlah:
Untuk mengevaluasi integral tersebut, misalkan . Akibatnya, dan . Dengan mensubstitusikan, diperoleh:
Dengan melambangkan fungsi densitas peluang normal baku sebagai , diperolehlah:
Jika kita definisikan zα adalah suatu bilangan nyata sedemikian hingga maka dengan memisalkan , ekspektasi permintaan yang tidak terpenuhi selama lead time dapat dinyatakan sebagai:
…………………………………………………………………………….. (3)
Pada halaman 144 karya Hadley dan Whitin [2] terdapat suatu teorema yang menyatakan bahwa , sehingga (3) dapat dinyatakan sebagai . Selanjutnya, dengan pemfaktoran diperoleh:
……………………………………………………………………………………….. (4)
Bahagia [1], dalam tabelnya di halaman 256 dan 257, secara implisit menggunakan lambang untuk menyatakan dan menamakannya sebagai ekspektasi parsial. Jadi, berdasarkan hal ini, ekspektasi parsial adalah . Dengan menggunakan notasi Bahagia [2] ini, persamaan (4) dapat dinyatakan sebagai . Karena σ = SL, persamaan terakhir ini dapat dinyatakan sebagai berikut.
…………………………………………………………………………………………………… (5)
Tetapi, di halaman 136, Bahagia [1] menyatakan N = SL[f(zα) – zαψ(zα)]. Ini perlu dikoreksi menjadi .
Berikut ini akan dilakukan pendekatan yang bertitik tolak dari karya Hadley dan Whitin [2] untuk menentukan ekspektasi banyaknya kekurangan persediaan selama lead time. Persamaan (4-15) di halaman 167 buku tersebut menyatakan sebagai berikut.
………………………………………………………………….. (6)
dengan r adalah reorder point dan h adalah fungsi densitas peluang normal dengan rata-rata µ dan simpangan baku σ. Dengan berpangkal pada (6), ekspektasi banyaknya kekurangan persediaan selama lead time, N, diperoleh dengan cara sebagai berikut.
Karena , selisih antara rata-rata banyaknya permintaan selama lead time dengan reorder point adalah . Dengan demikian N dapat dinyatakan sebagai berikut.
……………………………………………………………… (7)
Dengan mengkonversi lambang-lambang yang digunakan dalam (7) menjadi lambang-lambang yang digunakan oleh Bahagia [1], persamaan (7) dapat dinyatakan sebagai , yang tidak lain adalah persamaan (5), yaitu hasil yang diperoleh melalui pendekatan yang bertitik tolak pada proposisi Bahagia [1] seandainya penurunan rumusnya dilakukan dengan benar.
Dari seluruh uraian di atas, tampak bahwa jika evaluasi integral dalam (1) sebagaimana dinyatakan dinyatakan dalam Bahagia [1] dilakukan dengan benar, maka hasil yang diperoleh identik dengan hasil yang diperoleh apabila penurunan rumus bertitik tolak pada proposisi (6) yang terdapat dalam Hadley dan Whitin [2]. Keduanya menghasilkan , bukan sebagaimana dinyatakan Bahagia [1]. Perlu ditambahkan juga di sini, yaitu bahwa sebenarnya Bahagia [1] sudah menyatakan N dengan benar di persamaan (7-2) buku tersebut, yaitu . Di buku itu, . Dengan mensubstitusikan hasil ini ke dalam persamaan (7-2) buku tersebut, diperoleh , yang tidak lain adalah (7) apabila dalam (7) digunakan lambang-lambang yang.digunakan dalam Bahagia [1]. Dari uraian ini tampak bahwa Bahagia [1] mempersamakan α dengan sebagaimana nilai-nilainya terdapat dalam Tabel B buku tersebut, padahal α dan berbeda makna.
KESIMPULAN
Dari uraian di atas, diperoleh bahwa ekspektasi banyaknya kekurangan persediaan selama lead time adalah , dengan SL adalah simpangan baku permintaan selama lead time dan . Dalam formulasi ini, adalah fungsi densitas peluang normal baku, α adalah peluang terjadinya shortage selama lead time, dan zαadalah nilai z sedemikian hingga .
REFERENSI
[1] Bahagia, S. N. Sistem Inventori. Penerbit ITB. Bandung. 2006.
[2] Hadley, G. and Whitin, T. M. Analysis of Inventory Systems. Prentice-Hall, Inc. New York. 1963.
[3] Lati, G.M. dan Altavia, N. N. Pengendalian Biaya Persediaan Metoclopramide HCl di PT ZZZ Menggunakan Metode Economic Order Quantity (EOQ) Probabilistik. Jurnal Logistik Bisnis. 2022; Vol. 12 (2): 94-102.
[4] Setiadi, H. dan Raihan, S.N. Penerapan Kebijakan Persediaan Bahan Baku Kain Twist Menggunakan Metode EOQ Probabilistik Sederhana di PT Multi Garmenjaya. Jurnal Logistik Bisnis. 2020; Vol. 10 (2): 60-63.
[5] Syamil et. al. Penentuan Kebijakan Persediaan Produk Kategori Food dan Non-food Menggunakan Continuous Review (s,S) System dan (s,Q) System di PT XYZ untuk Oprimasi Biaya Persediaan. Jurnal Integrasi Sistem Industri UMJ. 2018; Vol. 05 (1).
KESALAHAN SANG PROFESOR
Model persediaan (inventory) probabilistik sederhana merupakan suatu perkembangan lebih lanjut dari model Economic Order Quantity yang dipelopori oleh Harris, dengan ciri bahwa permintaan terhadap produk bersifat probabilistik. Dengan tidak menentunya permintaan, mungkin terjadi kekurangan persediaan barang dalam masa ancang-ancang (lead time). Dalam literatur-literatur yang relevan salah satu materi yang menjadi perhatian adalah ekspektasi banyaknya kekurangan persediaan selama waktu ancang-ancang tersebut. Besarnya rata-rata kekurangan ini dibahas juga dalam sebuah buku berjudul Sistem Inventori yang ditulis oleh Senator Nur Bahagia, namun ternyata terdapat kesalahan di dalamnya. Artikel ini dibuat untuk memperbaiki kesalahan tersebut. Dua pendekatan yang telah dilakukan untuk menurunkan rumus ekspektasi shortage tersebut memberikan kesimpulan yang konsisten, yaitu bahwa terdapat kesalahan fatal dalam buku tersebut.
PENDAHULUAN
Salah satu kajian dalam bidang logistik adalah model-model persediaan, yang menurut Erlenkotter dipelopori pertama kali oleh Harris dengan model persediaannya Economic Order Quantity (EOQ) pada tahun 1913. Salah satu asumsi model ini adalah bahwa permintaan bersifat konstan, yang dalam praktik sangat jarang dijumpai. Perkembangan lebih lanjut dapat dilihat dalam Hadley dan Whitin [2], yang banyak mengurai berbagai model persediaan, termasuk model-model persediaan dengan pola permintaan yang bersifat stokastik.
Karya Hadley dan Whitin tersebut telah dijadikan rujukan oleh Bahagia [1] dalam membahas model probabilistik sederhana. Buku karangan Bahagia itu pun sering dijadikan rujukan dalam penelitian-penelitian di bidang persediaan, seperti dapat ditemukan dalam Setiadi dan Raihan [4], Lati dan Aktavia [3], dan Syamil et. al. [5]. Yang menjadi masalah adalah bahwa terdapat rumus yang salah yang ditulis Bahagia [1], yaitu rumus ekspektasi banyaknya kekurangan persediaan (shortage) pada persamaan (7-2) di halaman 136 buku tersebut. Mengingat buku tersebut banyak dijadikan rujukan dalam penelitian-penelitian di bidang persediaan, perlu dilakukan pembetulan terhadap kesalahan tersebut. Urgensi tersebutlah yang melatarbelakangi disusunnya artikel ini.
ASUMSI DAN METODE PENELITIAN
Asumsi yang digunakan dalam penelitian ini adalah: 1) selang waktu antara barang dipesan dan barang tiba, dinamakan lead time, bersifat konstan, 2) permintaan selama lead time berdistribusi normal dengan rata-rata DL dan simpangan baku SL, 3) pemesanan kembali (reorder) dilakukan pada saat tingkat persediaan mencapai r, dan 4) peluang terjadinya kekurangan persediaan selama lead time diketahui sebesar α. Berdasar pada asumsi-asumsi tersebut, penelitian ini akan menjawab berapakah ekspektasi banyaknya kekurangan persediaan selama lead time.
Penelitian ini dilakukan dengan beberapa tahap. Di tahap awal, penurunan rumus ekspektasi banyaknya kekurangan persediaan selama lead time dilakukan berdasarkan proposisi mengenai ekspektasi tersebut sebagaimana dinyatakan oleh Bahagia [1]. Tahap selanjutnya, penurunan rumus yang sama dilakukan dengan bertitik tolak pada salah satu proposisi dalam Hadley dan Whitin [2] sebagai salah satu literatur yang dirujuk oleh Bahagia [1]. Tahap terakhir yaitu menguji konsistensi hasil-hasil yang diperoleh dari kedua pendekatan tersebut.
HASIL DAN PEMBAHASAN
Menurut Bahagia [1], jika x menyatakan banyaknya permintaan selama lead time, r = reorder point, dan f adalah fungsi densitas peluang banyaknya permintaan selama lead time, maka ekspektasi permintaan yang tidak terpenuhi selama lead time, yang untuk selanjutnya dilambangkan dengan N, dapat dinyatakan sebagai berikut.
Berdasarkan asumsi penelitian nomor 2, yaitu bahwa permintaan selama lead time berdistribusi normal dengan rata-rata DL dan simpangan baku SL, diperolehlah f(x) = n(x; DL, SL), dengan n(x; DL, SL) menyatakan fungsi densitas peluang normal dengan rata-rata DL dan simpangan baku SL sehingga (1) dapat dinyatakan sebagai:
Untuk menyederhanakan notasi, untuk selanjutnya penulisan DL disederhanakan menjadi μ dan SL disederhanakan menjadi σ. Jadi, (2) dapat dinyatakan sebagai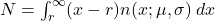 . Selanjutnya, dengan mensubstitusikan
. Selanjutnya, dengan mensubstitusikan 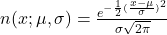 ke dalam (2), diperolehlah:
ke dalam (2), diperolehlah:
Untuk mengevaluasi integral tersebut, misalkan . Akibatnya,
. Akibatnya,  dan
dan  . Dengan mensubstitusikan, diperoleh:
. Dengan mensubstitusikan, diperoleh:
Dengan melambangkan fungsi densitas peluang normal baku sebagai , diperolehlah:
, diperolehlah:
Jika kita definisikan zα adalah suatu bilangan nyata sedemikian hingga maka dengan memisalkan
maka dengan memisalkan  , ekspektasi permintaan yang tidak terpenuhi selama lead time dapat dinyatakan sebagai:
, ekspektasi permintaan yang tidak terpenuhi selama lead time dapat dinyatakan sebagai:
Pada halaman 144 karya Hadley dan Whitin [2] terdapat suatu teorema yang menyatakan bahwa , sehingga (3) dapat dinyatakan sebagai
, sehingga (3) dapat dinyatakan sebagai 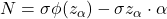 . Selanjutnya, dengan pemfaktoran diperoleh:
. Selanjutnya, dengan pemfaktoran diperoleh:
Bahagia [1], dalam tabelnya di halaman 256 dan 257, secara implisit menggunakan lambang untuk menyatakan
untuk menyatakan 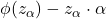 dan menamakannya sebagai ekspektasi parsial. Jadi, berdasarkan hal ini, ekspektasi parsial adalah
dan menamakannya sebagai ekspektasi parsial. Jadi, berdasarkan hal ini, ekspektasi parsial adalah 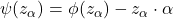 . Dengan menggunakan notasi Bahagia [2] ini, persamaan (4) dapat dinyatakan sebagai
. Dengan menggunakan notasi Bahagia [2] ini, persamaan (4) dapat dinyatakan sebagai  . Karena σ = SL, persamaan terakhir ini dapat dinyatakan sebagai berikut.
. Karena σ = SL, persamaan terakhir ini dapat dinyatakan sebagai berikut.
Tetapi, di halaman 136, Bahagia [1] menyatakan N = SL[f(zα) – zαψ(zα)]. Ini perlu dikoreksi menjadi .
.
Berikut ini akan dilakukan pendekatan yang bertitik tolak dari karya Hadley dan Whitin [2] untuk menentukan ekspektasi banyaknya kekurangan persediaan selama lead time. Persamaan (4-15) di halaman 167 buku tersebut menyatakan sebagai berikut.
dengan r adalah reorder point dan h adalah fungsi densitas peluang normal dengan rata-rata µ dan simpangan baku σ. Dengan berpangkal pada (6), ekspektasi banyaknya kekurangan persediaan selama lead time, N, diperoleh dengan cara sebagai berikut.
Karena , selisih antara rata-rata banyaknya permintaan selama lead time dengan reorder point adalah
, selisih antara rata-rata banyaknya permintaan selama lead time dengan reorder point adalah  . Dengan demikian N dapat dinyatakan sebagai berikut.
. Dengan demikian N dapat dinyatakan sebagai berikut.
Dengan mengkonversi lambang-lambang yang digunakan dalam (7) menjadi lambang-lambang yang digunakan oleh Bahagia [1], persamaan (7) dapat dinyatakan sebagai , yang tidak lain adalah persamaan (5), yaitu hasil yang diperoleh melalui pendekatan yang bertitik tolak pada proposisi Bahagia [1] seandainya penurunan rumusnya dilakukan dengan benar.
, yang tidak lain adalah persamaan (5), yaitu hasil yang diperoleh melalui pendekatan yang bertitik tolak pada proposisi Bahagia [1] seandainya penurunan rumusnya dilakukan dengan benar.
Dari seluruh uraian di atas, tampak bahwa jika evaluasi integral dalam (1) sebagaimana dinyatakan dinyatakan dalam Bahagia [1] dilakukan dengan benar, maka hasil yang diperoleh identik dengan hasil yang diperoleh apabila penurunan rumus bertitik tolak pada proposisi (6) yang terdapat dalam Hadley dan Whitin [2]. Keduanya menghasilkan , bukan
, bukan ![Rendered by QuickLaTeX.com N = S_L [f(z_{\alpha}) - z_{\alpha} \psi (z_{\alpha})]](https://edscyclopedia.com/wp-content/ql-cache/quicklatex.com-d781dfe10126503f8f1dd24ef5abb491_l3.png) sebagaimana dinyatakan Bahagia [1]. Perlu ditambahkan juga di sini, yaitu bahwa sebenarnya Bahagia [1] sudah menyatakan N dengan benar di persamaan (7-2) buku tersebut, yaitu
sebagaimana dinyatakan Bahagia [1]. Perlu ditambahkan juga di sini, yaitu bahwa sebenarnya Bahagia [1] sudah menyatakan N dengan benar di persamaan (7-2) buku tersebut, yaitu ![Rendered by QuickLaTeX.com N = S_L [f(z_{\alpha} ) - z_{\alpha} \Psi (z_{\alpha})]](https://edscyclopedia.com/wp-content/ql-cache/quicklatex.com-eb6a0eed43ecf4ab860c97b6f9981aac_l3.png) . Di buku itu,
. Di buku itu,  . Dengan mensubstitusikan hasil ini ke dalam persamaan (7-2) buku tersebut, diperoleh
. Dengan mensubstitusikan hasil ini ke dalam persamaan (7-2) buku tersebut, diperoleh ![Rendered by QuickLaTeX.com N = S_L [f(z_{\alpha}) - z_{\alpha} \cdot \alpha]](https://edscyclopedia.com/wp-content/ql-cache/quicklatex.com-cecbb5e693d230801cc6dd3eb14860e9_l3.png) , yang tidak lain adalah (7) apabila dalam (7) digunakan lambang-lambang yang.digunakan dalam Bahagia [1]. Dari uraian ini tampak bahwa Bahagia [1] mempersamakan α dengan
, yang tidak lain adalah (7) apabila dalam (7) digunakan lambang-lambang yang.digunakan dalam Bahagia [1]. Dari uraian ini tampak bahwa Bahagia [1] mempersamakan α dengan 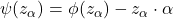 sebagaimana nilai-nilainya terdapat dalam Tabel B buku tersebut, padahal α dan
sebagaimana nilai-nilainya terdapat dalam Tabel B buku tersebut, padahal α dan  berbeda makna.
berbeda makna.
KESIMPULAN
Dari uraian di atas, diperoleh bahwa ekspektasi banyaknya kekurangan persediaan selama lead time adalah , dengan SL adalah simpangan baku permintaan selama lead time dan
, dengan SL adalah simpangan baku permintaan selama lead time dan 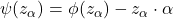 . Dalam formulasi ini,
. Dalam formulasi ini,  adalah fungsi densitas peluang normal baku, α adalah peluang terjadinya shortage selama lead time, dan zα adalah nilai z sedemikian hingga
adalah fungsi densitas peluang normal baku, α adalah peluang terjadinya shortage selama lead time, dan zα adalah nilai z sedemikian hingga  .
.
REFERENSI
[1] Bahagia, S. N. Sistem Inventori. Penerbit ITB. Bandung. 2006.
[2] Hadley, G. and Whitin, T. M. Analysis of Inventory Systems. Prentice-Hall, Inc. New York. 1963.
[3] Lati, G.M. dan Altavia, N. N. Pengendalian Biaya Persediaan Metoclopramide HCl di PT ZZZ Menggunakan Metode Economic Order Quantity (EOQ) Probabilistik. Jurnal Logistik Bisnis. 2022; Vol. 12 (2): 94-102.
[4] Setiadi, H. dan Raihan, S.N. Penerapan Kebijakan Persediaan Bahan Baku Kain Twist Menggunakan Metode EOQ Probabilistik Sederhana di PT Multi Garmenjaya. Jurnal Logistik Bisnis. 2020; Vol. 10 (2): 60-63.
[5] Syamil et. al. Penentuan Kebijakan Persediaan Produk Kategori Food dan Non-food Menggunakan Continuous Review (s,S) System dan (s,Q) System di PT XYZ untuk Oprimasi Biaya Persediaan. Jurnal Integrasi Sistem Industri UMJ. 2018; Vol. 05 (1).
Bagikan ini:
Most visitors also read :
DISTRIBUSI NORMAL DALAM ILMU KOMUNIKASI
DISTRIBUSI BINOMIAL DALAM ILMU KOMUNIKASI
TAFSIRAN GEOMETRIS KOMPONEN UTAMA
KOMPONEN UTAMA POPULASI (POPULATION PRINCIPAL COMPONENTS)