UJI KOLMOGOROV-SMIRNOV
Sebagian peneliti sering salah menafsirkan kegunaan Uji Kolmogorov-Smirnov dengan mengidentikkannya dengan uji normalitas. Padahal, secara umum uji Kolmogorov-Smirnov digunakan untuk memeriksa apakah data hasil sampling tertentu berasal dari suatu populasi dengan distribusi peluang teoretis tertentu. Distribusi peluang teoretis yang dimaksud di sini adalah sembarang distribusi peluang teoretis yang kontinu, seperti distribusi normal, distribusi eksponensial, distribusi Weibull, distribusi gamma, dan sebagainya. Jadi, tidak benar apabila dikatakan bahwa uji ini hanya untuk menguji apakah suatu populasi berdistribusi normal atau tidak. Juga tidak benar apabila dikatakan bahwa satu-satunya cara menguji normalitas dengan uji Kolmogorov-Smirnov. Ada cara lain melakukan uji normalitas, di antaranya dengan Chi-Square Test, Anderson-Darling Test.
Hipotesis nol dan hipotesis tandingan dalam uji ini adalah sebagai berikut.
H0: F(x) = F0(x)
H1: F(x) ≠ F0(x)
Dengan kata-kata, dapat ditulis misalnya
H0: Tinggi badan berdistribusi normal
H1: Tinggi badan tidak berdistribusi normal
atau misalnya
H0: Selang waktu antarkedatangan pelanggan berdistribusi eksponensial
H1: Selang waktu antarkedatangan pelanggan tidak berdistribusi eksponensial
Uji ini mengasumsikan distribusi yang mendasari variabel yang diuji bersifat kontinu sebagaimana ditentukan/dinyatakan oleh distribusi frekuensi kumulatifnya. Jadi, uji ini cocok untuk menguji kebaikan-suai (goodness-of-fit) bagi variabel-variabel yang diukur dengan tingkat ordinal atau tingkat yang lebih tinggi.
Statistik uji yang digunakan adalah penyimpangan maksimum, D, yang didefinisikan sebagai berikut.
![]()
dengan:
F0(x) = frekuensi relatif kumulatif yang dihitung menggunakan distribusi teoretis sebagaimana dnyatakan dalam hipotesis nol.
Fn(x) = frekuensi relatif kumulatif yang dihitung menggunakan distribusi empiris (yang sedang diuji)
Untuk menghitung D, perlu didefinisikan terlebih dahulu:
![]()
; dengan Fk adalah banyaknya pengamatan yang nilainya tidak melebihi yk.
Apabila y1, y2, y3, …, yn adalah data hasil sampling yang telah diurutkan sedemikian hingga y1 ≤ y2 ≤ y3 ≤ … ≤ yn, nilai D secara teknis dapat ditentukan dengan rumus:
![]()
Penggunaan tabel sebagaimana dicontohkan di bawah, akan mempermudah perhitungan D di atas.
Untuk menguji signifikansi uji ini, digunakanlah Tabel Nilai Kritis D dalam Uji Satu-Sampel Kolmogorov-Smirnov, yaitu untuk menentukan daerah penolakan H0 dengan taraf nyata tertentu. Jika nilai D hasil perhitungan terletak di daerah kritis, kita tolak H0 dan kita simpulkan populasi yang kita amati tersebut tidak berdistribusi sebagaimana yang dinyatakan dalam H0.
Contoh:
Hasil sampling tinggi badan 10 orang siswa di suatu sekolah (dalam satuan cm) adalah sebagai berikut: 165, 163, 167, 166, 159, 167, 167, 169, 172, 165. Apakah cukup bukti untuk menyatakan bahwa sampel tersebut tidak berasal dari populasi yang tingginya berdistribusi normal dengan rata-rata 166 cm dan simpangan baku 3,464 cm? Gunakan taraf nyata 0,05.
Jawab:
H0: Tinggi badan siswa di sekolah itu berdistribusi normal dengan rata-rata 166 cm dan simpangan baku 3,464 cm
H1: Tinggi badan siswa di sekolah itu tidak berdistribusi normal dengan rata-rata 166 cm dan simpangan baku 3,464 cm
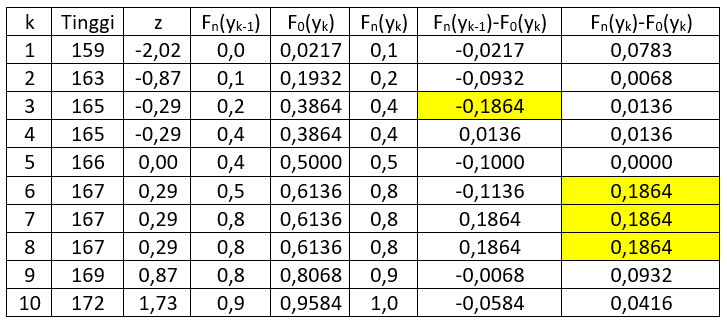
Untuk memudahkan, kita urutkan ke-10 data tersebut dari yang terkecil sampai terbesar, sehingga y1 = 159, y2 = 163, y3 = y4 = 165, y5 = 166, y6 = y7 = y8 = 167, y9 = 169, dan y10 = 172.
Frekuensi relatif kumulatif untuk masing-masing yk (i = 1, 2, 3, …, 10) adalah sebagai berikut.

Fi untuk masing-masing yk dihitung sebagai berikut:
F1 = 1 karena terdapat 1 buah data yang nilainya ≤ y1 = 159
F2 = 2 karena terdapat 2 buah data yang nilainya ≤ y2 = 163, yaitu y1 dan y2
F3 = 4 karena terdapat 4 buah data yang nilainya ≤ y3 = 165, yaitu y1, y2, y3, dan y4
F4 = 4 karena terdapat 4 buah data yang nilainya ≤ y4 = 165, yaitu y1, y2, y3, dan y4
F5 = 5 karena terdapat 5 buah data yang nilainya ≤ y5 = 166, yaitu y1, y2, y3, y4, dan y5
F6 = F7 = F8 = 8 karena terdapat 8 data yang nilainya ≤ y6 = y7 = y8 = 167 yaitu y1 hingga y8
F9 = 9 karena terdapat 9 data yang nilainya ≤ y9 = 169, yaitu y1 hingga y9
F10 = 10 karena terdapat 10 data yang nilainya ≤ y10 = 172, yaitu y1 hingga y10
Menggunakan rumus (+), diperolehlah:
F10(y1) = F10(159) = 1/10 = 0,1
F10(y2) = F10(163) = 2/10 = 0,2
F10(y3) = F10(y4) = F10(165) = 4/10 = 0,4
F10(y5) = F10(166) = 5/10 = 0,5
F10(y6) = F10(y7) = F10(y8) = F10(167) = 8/10 = 0,8
F10(y9) = F10(169) = 9/10 = 0,9
F10(y10) = F10(172) = 10/10 = 1,0
Hasil-hasil tersebut dapat diringkaskan pada tabel berikut.
Tabel 1
Catatan:
Kolom z di atas ditampilkan untuk keperluang menghitung F0(yk), yaitu frekuensi relatif kumulatif hingga y = yk dengan menggunakan distribusi peluang sebagaimana dinyatakan dalam H0. Sebagai contoh, karena dalam kasus ini distribusi normal merupakan distribusi peluang teoretis pada H0, maka:Catatan:
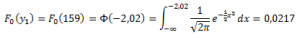
Dengan cara serupa akan diperoleh F0(y2), dan seterusnya, hingga F0(y10). [Lihat Tabel 1 di atas.]
Apabila semua bilangan di kedua kolom terkanan tabel di atas diambil harga mutlaknya, diperoleh tabel berikut.
Tabel 2
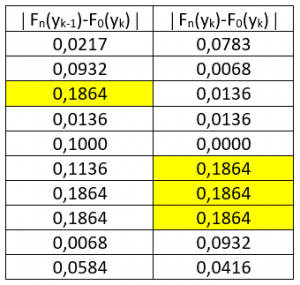
Bilangan terbesar di antara kedua kolom pada tabel terakhir adalah nilai statistik D dari Uji Kolmogorov-Smirnov. Jadi, D = 0,1864
Dari Tabel Nilai Kritis D dalam Uji Satu-Sampel Kolmogorov-Smirnov dengan n = 10 dan α = 0,05, diperoleh nilai kritis D0,05;10 = 0,409 dan karena D < D0,05;10 kita tak dapat menolak H0. Hasil sampling yang ada tidak cukup untuk menyangkal pernyataan bahwa populasi tinggi badan siswa di sekolah itu berdistribusi normal dengan rata-rata 166 cm dan simpangan baku 3,464 cm.
Sebagai perbandingan, saya tampilkan hasil pengujian di atas dengan menggunakan SPSS:

Catatan: [mengenai hasil SPSS di atas]
- Bilangan -0,186 pada tabel tersebut merupakan bilangan negatif terkecil di kolom Fn(yk-1) – F0(yk) pada Tabel 1 di atas.
- Nilai Positive 0,186 pada tabel tersebut merupakan bilangan positif terbesar di kolom Fn(yk) – F0(yk) pada Tabel 1 di atas.
- Nilai Absolute 0,186 adalah nilai D sebagaimana dimaksud pada rumus:
![]() yaitu bilangan terbesar di antara kedua kolom pada Tabel 2.
yaitu bilangan terbesar di antara kedua kolom pada Tabel 2.
4. Nilai Kolmogorov-Smirnov Z sebesar 0,589 diperoleh dari:
![]()
Pengayaan
Berikut ini adalah perintah-perintah dalam perangkat lunak statistika R, untuk melakukan uji Kolmogorov-Smirnov pada contoh di atas.
> tinggi<-c(159,163,165,165,166,167,167,167,169,172)
> ks.test(tinggi,”pnorm”,mean(tinggi),sd(tinggi))
Hasil yang diperoleh adalah sebagai berikut:

Berikut ini adalah tautan-tautan yang terkait dengan Uji Kolmogorov-Smirnov.
- Tabel Nilai Kritis D Kolmogorov-Smirnov
- File Excel untuk menghitung statistik D Kolmogorov-Smirnov yang digunakan untuk perhitungan pada contoh dalam tulisan ini
- Contoh-contoh kasus lain mengenai goodness-of-fit dengan Uji Kolmogorov-Smirnov: (belum tersedia)
- Bagaimana apabila parameter-parameter distribusi peluang yang dihipotesiskan tidak diketahui? Uji Lilliefors adalah solusinya. (belum tersedia)




Assalamualaikum
maaf ka mau nanya nih, kan untuk menguji normalitas itu ada yang pakai shapiro dan kolmogorov.. trus bedanya iyu apa antara keduanya??
Pak saya mau bertanya, kalau untuk uji distribusi Poisson dan distribusi eksponensial menggunakan KS-Test stepnya seperti apa ya? terima kasih banyak
Pengujian Distribusi Poisson tidak bisa dengan KS test karena KS test hanya untuk pengujian distribusi kontinu, sedangkan Distr Poisson diskrit. Untuk pengujian distr. eksponensial caranya sama, yang beda hanya fungsi densitas peluang yang digunakan. Demikian.
terima kasih atas jawabannya pak. tapi di SPSS disediakan KS_Test untuk Uniform dan Poisson itu bagaimana ya pak?
Dengan menggunakan SPSS kita dapat juga menguji apakah suatu sampel berasal dari populasi yang berdistribusi uniform atau tidak. Untuk menguji hal tersebut, dapat digunakan uji Kolmogorov-Smirnov.