Di post yang lalu, kita telah belajar suatu distribusi peluang diskrit yang dinamakan distribusi binomial. Jika X adalah variabel acak yang menunjukkan banyaknya keberhasilan dalan suatu proses Bernoulli maka besarnya peluang X = x adalah , dengan n adalah banyaknya perulangan dan p adalah peluang keberhasilan. Nilai-nilai n dan p menentukan “bentuk” distribusi ini. Keduanya merupakan parameter-parameter distribusi binomial.
Untuk melihat bagaimana kedua parameter tersebut berpengaruh terhadap bentuk distribusi, mari kita visualisasikan histogram peluang binomial dengan berbagai nilai n dan p menggunakan perangkat lunak R.
Percobaan 1: n = 11, p = 0,67
Ketikkan kode R berikut:
x <- seq(0,11,by = 1)
y <- dbinom(x,11,0.67)
plot(x,y,type=”h”,ylab=”B(x;11,0.67)”)
Kode tersebut akan menghasilkan grafik berikut. Lihat Gambar 1.
Gambar 1
Berikutnya, dengan Percobaan 2, kita memperbanyak n menjadi 30.
Percobaan 1: n = 30, p = 0,67
Ketikkan kode R berikut:
x <- seq(0,30,by = 1)
y <- dbinom(x,30,0.67)
plot(x,y,type=”h”,ylab=”B(x;30,0.67)”)
Kode tersebut akan menghasilkan grafik berikut. Lihat Gambar 2.
Gambar 2
Selanjutnya, tambah lagi nilai n menjadi 50. Ketikkan kode R yang cocok. Jika kode tersebut benar maka akan diperoleh grafik seperti pada Gambar 3.
Gambar 3
Dengan semakin bertambah besarnya nilai n, grafik yang terbentuk semakin menyerupai bentuk lonceng/bel. Untuk n = 100, grafiknya diperlihatkan Gambar 4.
Gambar 4
Jika n semakin besar menuju tak berhingga maka bentuk hampiran distribusi binomial tersebut adalah distribusi normal baku, sebagaimana dituangkan pada teorema berikut.
Teorema
Jika X merupakan variabel acak binomial dengan rata-rata μ = np dan variansi σ2 = np(1-p) maka bentuk hampiran distribusi apabila adalah distribusi normal baku.
Distribusi normal baku memiliki fungsi densitas peluang. Distribusi tersebut memiliki rata-rata = 0 dan simpangan baku = 1. Berikut adalah grafik kurva normal baku.
Gambar 5
Pada Gambar 5, sumbu mendatarnya mewakili nilai-nilai z. Jadi, setiap titik pada kurva tersebut memiliki koordinat (z,n(z)). Titik A dan B pada Gambar 5 menunjukkan letak titik belok kurva. Proyeksi kedua titik tersebut pada sumbu mendatar adalah titik-titik z = -1 dan z = 1. Titik belok kurva terjadi pada nilai z yang harga mutlaknya merupakan simpangan baku distribusi ini, yaitu 1. Selanjutnya, perhatikan bahwa kurva tersebut simetris terhadap suatu sumbu tegak, yaitu suatu garis dengan persamaan z = 0. Nilai 0 ini menunjukkan rata-rata dari distribusi normal baku. Distribusi normal baku memiliki rata-rata = 0 dan simpangan baku = 1.
Walaupun pada Gambar 5 tampak bahwa kurva berpotongan dengan sumbu mendatar (sumbu z), namun, dengan analisis terhadap persamaan kurva n(z) di atas, sebenarnya kurva tidak akan berpotongan dengan sumbu mendatar. Semakin ke kiri, titik-titik pada kurva semakin mendekat sumbu z. Demikian juga semakin ke kanan. Sumbu z merupakan garis asimtot mendatar kurva normal baku.
Sifat lainnya yang dimiliki kurva normal baku adalah mengenai luas daerah di bawah kurva. Luas total daerah yang terletak di antara kurva dan sumbu z adalah 1 (Lihat Gambar 6.)
Gambar 6
Jadi, total luas daerah di bawah kurva normal baku adalah .
Selain distribusi normal baku, terdapat suatu distribusi normal yang lebih umum, yaitu yang memiliki rata-rata dan simpangan baku . Fungsi densitas peluangnya dapat dinyatakan sebagai . Tentang ini dapat dipelajari lebih lanjut di tautan berikut: (klik di sini).
BERKENALAN DENGAN DISTRIBUSI NORMAL BAKU
Di post yang lalu, kita telah belajar suatu distribusi peluang diskrit yang dinamakan distribusi binomial. Jika X adalah variabel acak yang menunjukkan banyaknya keberhasilan dalan suatu proses Bernoulli maka besarnya peluang X = x adalah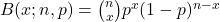 , dengan n adalah banyaknya perulangan dan p adalah peluang keberhasilan. Nilai-nilai n dan p menentukan “bentuk” distribusi ini. Keduanya merupakan parameter-parameter distribusi binomial.
, dengan n adalah banyaknya perulangan dan p adalah peluang keberhasilan. Nilai-nilai n dan p menentukan “bentuk” distribusi ini. Keduanya merupakan parameter-parameter distribusi binomial.
Untuk melihat bagaimana kedua parameter tersebut berpengaruh terhadap bentuk distribusi, mari kita visualisasikan histogram peluang binomial dengan berbagai nilai n dan p menggunakan perangkat lunak R.
Percobaan 1: n = 11, p = 0,67
Ketikkan kode R berikut:
x <- seq(0,11,by = 1)
y <- dbinom(x,11,0.67)
plot(x,y,type=”h”,ylab=”B(x;11,0.67)”)
Kode tersebut akan menghasilkan grafik berikut. Lihat Gambar 1.
Berikutnya, dengan Percobaan 2, kita memperbanyak n menjadi 30.
Percobaan 1: n = 30, p = 0,67
Ketikkan kode R berikut:
x <- seq(0,30,by = 1)
y <- dbinom(x,30,0.67)
plot(x,y,type=”h”,ylab=”B(x;30,0.67)”)
Kode tersebut akan menghasilkan grafik berikut. Lihat Gambar 2.
Gambar 2
Selanjutnya, tambah lagi nilai n menjadi 50. Ketikkan kode R yang cocok. Jika kode tersebut benar maka akan diperoleh grafik seperti pada Gambar 3.
Gambar 3
Dengan semakin bertambah besarnya nilai n, grafik yang terbentuk semakin menyerupai bentuk lonceng/bel. Untuk n = 100, grafiknya diperlihatkan Gambar 4.
Gambar 4
Jika n semakin besar menuju tak berhingga maka bentuk hampiran distribusi binomial tersebut adalah distribusi normal baku, sebagaimana dituangkan pada teorema berikut.
Teorema
Jika X merupakan variabel acak binomial dengan rata-rata μ = np dan variansi σ2 = np(1-p) maka bentuk hampiran distribusi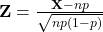 apabila
apabila 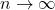 adalah distribusi normal baku.
adalah distribusi normal baku.
Distribusi normal baku memiliki fungsi densitas peluang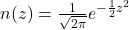 . Distribusi tersebut memiliki rata-rata = 0 dan simpangan baku = 1. Berikut adalah grafik kurva normal baku.
. Distribusi tersebut memiliki rata-rata = 0 dan simpangan baku = 1. Berikut adalah grafik kurva normal baku.
Gambar 5
Pada Gambar 5, sumbu mendatarnya mewakili nilai-nilai z. Jadi, setiap titik pada kurva tersebut memiliki koordinat (z,n(z)). Titik A dan B pada Gambar 5 menunjukkan letak titik belok kurva. Proyeksi kedua titik tersebut pada sumbu mendatar adalah titik-titik z = -1 dan z = 1. Titik belok kurva terjadi pada nilai z yang harga mutlaknya merupakan simpangan baku distribusi ini, yaitu 1. Selanjutnya, perhatikan bahwa kurva tersebut simetris terhadap suatu sumbu tegak, yaitu suatu garis dengan persamaan z = 0. Nilai 0 ini menunjukkan rata-rata dari distribusi normal baku. Distribusi normal baku memiliki rata-rata = 0 dan simpangan baku = 1.
Walaupun pada Gambar 5 tampak bahwa kurva berpotongan dengan sumbu mendatar (sumbu z), namun, dengan analisis terhadap persamaan kurva n(z) di atas, sebenarnya kurva tidak akan berpotongan dengan sumbu mendatar. Semakin ke kiri, titik-titik pada kurva semakin mendekat sumbu z. Demikian juga semakin ke kanan. Sumbu z merupakan garis asimtot mendatar kurva normal baku.
Sifat lainnya yang dimiliki kurva normal baku adalah mengenai luas daerah di bawah kurva. Luas total daerah yang terletak di antara kurva dan sumbu z adalah 1 (Lihat Gambar 6.)
Gambar 6
Jadi, total luas daerah di bawah kurva normal baku adalah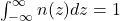 .
.
Selain distribusi normal baku, terdapat suatu distribusi normal yang lebih umum, yaitu yang memiliki rata-rata dan simpangan baku
dan simpangan baku 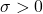 . Fungsi densitas peluangnya dapat dinyatakan sebagai
. Fungsi densitas peluangnya dapat dinyatakan sebagai 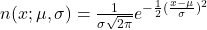 . Tentang ini dapat dipelajari lebih lanjut di tautan berikut: (klik di sini).
. Tentang ini dapat dipelajari lebih lanjut di tautan berikut: (klik di sini).
Bagikan ini:
Most visitors also read :
PENGUJIAN VALIDITAS KUESIONER DENGAN CARA SEDERHANA
PENDAHULUAN REGRESI LINIER BERGANDA
BERKENALAN DENGAN REGRESI LINIER SEDERHANA
KOEFISIEN KORELASI SPEARMAN’S RHO