UJI HIPOTESIS RATA-RATA SATU-SAMPEL DALAM ILMU KOMUNIKASI (1)
April 4th, 2025
Kata “hipotesis” memang jarang ditemukan dalam percakapan sehari-hari. Walaupun demikian, kita sering mendengar kata “dugaan”. Jika suatu hal merupakan suatu dugaan maka hal tersebut belum tentu benar. Untuk mengetahui apakah yang diduga itu benar, kita melakukan penyelidikan. Demikian juga dengan hipotesis. Pada dasarnya, hal yang dihipotesiskan belum tentu benar adanya. Dalam statistika, penyusunan hipotesis perlu ditindaklanjuti dengan penarikan sampel. Jika hasil sampling berhasil membuktikan bahwa hipotesis tersebut keliru maka hipotesis ditolak.
Berikut ini adalah beberapa contoh kasus yang menggambarkan secara sederhana bagaimana uji hipotesis diterapkan dalam ilmu komunikasi.
Kasus 1
Seorang peneliti komunikasi berpendapat bahwa peningkatan waktu yang dihabiskan di media sosial mengakibatkan penurunan keterampilan komunikasi tatap muka di kalangan dewasa muda. Mereka menyusun hipotesis bahwa rata-rata skor keterampilan komunikasi tatap muka (diukur pada skala standar) untuk dewasa muda yang menghabiskan lebih dari 3 jam setiap hari di media sosial lebih rendah daripada skor rata-rata nasional yaitu 75. Berikut adalah sampel yang diambil untuk memeriksa hipotesis tersebut, dalam format .sav: (klik di sini). Pada taraf nyata 0,05, apakah sampel mendukung hipotesis bahwa rata-rata skor lebih rendah dari 75?
Berikut ini akan diuraikan langkah-langkah yang diperlukan untuk menjawab pertanyaan pada Kasus 1.
Penjelasan Langkah 1 Dalam uji hipotesis statistik, hipotesis dibuat berpasangan, yaitu hipotesis nol (H0) dan hipotesis tandingan/alternatif (H1).Pernyataan dalam H1 adalah pernyataan yang akan dijadikan kesimpulan apabila nanti H0 ditolak. Tanda relasi yang digunakan dalam hipotesis alternatif harus salah satu di antara <, >, atau ≠. Dalam kasus ini, yang akan dibuktikan dalam kasus ini adalah rata-rata skor keterampilan komunikasi tatap muka dewasa muda yang menghabiskan lebih dari 3 jam setiap hari di media sosial lebih rendah daripada skor rata-rata nasional (yaitu 75). Karena itu, pernyataan dalam H1 adalah μ < 75. Relasi yang digunakan dalam H0 adalah sangkalan/ingkaran dari relasi yang digunakan dalam H1. Jadi, pada kasus ini, pernyataan dalam H0 adalah μ ≥ 75.
Langkah 2: Menentukan taraf nyata (α)
Pada kasus ini, taraf nyata telah ditentukan, yaitu sebesar 0,05. Dalam praktik penelitian sesungguhnya, taraf nyata ditentukan oleh peneliti itu sendiri. Taraf nyata adalah peluang terjadinya kesalahan apabila nanti terjadi penolakan hipotesis nol. Dalam kasus ini, jika nanti hipotesis nol ditolak, maka kesimpulannya adalah rata-rata skor keterampilan komunikasi tatap muka dewasa muda yang menghabiskan lebih dari 3 jam setiap hari di media sosial lebih rendah daripada skor rata-rata nasional dan peluang kita salah dalam menyimpulkan ini hanya sebesar 5%.
Langkah 3: Menentukan statistik uji dan daerah penolakan
Statistik uji yang digunakan pada kasus ini adalah dengan derajat kebebasan . Statistik ini digunakan apabila populasi berdistribusi normal. Dalam teori, terdapat dua statistik lain, yaitu dan . Namun, statistik jarang digunakan dalam praktik karena dalam praktik, (simpangan baku populasi) jarang diketahui. (Data pada kasus ini sudah dirancang sedemikian rupa sehingga dapat dianggap bahwa populasi berdistribusi normal, sehingga statistik t dapat digunakan.)
Untuk menentukan daerah penolakan, pertama-tama tentukan dulu nilai kritis t-nya. Di salah satu sel lembar Excel, ketikkan: =T.INV(0.05;99). Lihat Gambar 1.
Gambar 1
Setelah tombol Enter ditekan, Excel akan memunculkan nilai -1,660 (apabila dibulatkan hingga 3 tempat desimal). Selanjutnya, daerah penolakan dapat digambarkan sebagai berikut.
Gambar 2
Pada Gambar 2, daerah penolakan ditunjukkan dengan daerah berarsir biru muda. Daerah ini terletak di sisi kiri. Karena itulah uji ini dinamakan uji ekor kiri. Dalam uji ini digunakan ekor kiri karena dalam hipotesis tandingan, digunakan tanda < (lebih kecil dari). Manfaat penentuan daerah penolakan ini adalah untuk memutuskan apakah cukup bukti untuk menolak H0. Apabila nilai t hasil perhitungan (yang diperoleh dari sampel) memiliki nilai kurang dari -1,660 (jatuh di daerah penolakan) maka H0 ditolak.
Langkah 4: Menghitung nilai t dari sampel
Nilai t dari sampel diperoleh dengan menggunakan rumus . Tabel berikut menampilkan hasil pengolahan data menggunakan SPSS. (Untuk mengetahui bagaiamana cara menampilkan output SPSS berikut, klik di sini.)
TABEL OUTPUT SPSS
Dari tabel di atas kita mendapatkan nilai t hasil perhitungan (computed t-value, thitung), yaitu sebesar -4,208 dan nilai ini lebih kecil dari nilai kritisnya (yaitu -1,660).
Langkah 5: Penarikan kesimpulan
Nilai thitung pada kasus ini, yaitu -4,208, jatuh di daerah penolakan. Lihat Gambar 3.
Gambar 3
Karena itu, kita menolak hipotesis nol dan selanjutnya menerima hipotesis tandingannya.
KESIMPULAN:Rata-rata skor keterampilan komunikasi tatap muka untuk dewasa muda yang menghabiskan lebih dari 3 jam setiap hari di media sosial secara signifikan lebih rendah daripada skor rata-rata nasional. Peneliti tersebut berhasil mendukung pendapatnya, yaitu bahwa peningkatan waktu yang dihabiskan di media sosial mengakibatkan penurunan keterampilan komunikasi tatap muka di kalangan dewasa muda.
Catatan Hasil uji hipotesis mungkin signifikan, mungkin juga tidak signifikan.Jika kita berhasil menolak H0 maka uji tersebut dikatakan signifikan dan besarnya peluang terjadi kesalahan dalam penolakan ini adalah sebesar α. Sebaliknya, jika kita gagal menolak H0 maka uji itu dikatakan tidak signifikan. Dalam hal tidak terjadi penolakan H0, besarnya peluang terjadi kesalahan dalam penyimpulan tersebut tidak dapat ditentukan. Dalam Kasus 1, kita berhasil menolak hipotesis nol, sehingga dalam kesimpulannya terdapat frasa “secara signifikan”. Peluang kita salah memberikan kesimpulan ini adalah sebesar taraf nyatanya. Jadi, peluang peneliti tersebut salah menyimpulkan adalah 5%.
CARA LAIN MENARIK KESIMPULAN
Selain menggunakan nilai kritis, terdapat cara lain untuk membuat kesimpulan, yaitu dengan menggunakan nilai-p (p-value). Cara ini kadang-kadang lebih disukai karena cara ini “menghilangkan” Langkah 3 di atas. Dengan cara nilai-p ini, aturan penolakan H0 adalah sebagai berikut: Tolak H0 apabila p < α. Jangan tolak H0 apabila p > α.
Bagaimana menggunakan nilai-p pada Kasus 1? Perhatikan bagian TABEL OUTPUT SPSS di atas yang berjudul One-Sample Test. Di kolom yang berjudul Sig.(2-tailed), terdapat angka 5.662E-005, yaitu 0,00005662. Nilai yang ditunjukkan tersebut merupakan nilai-p untuk uji 2 ekor (2-tailed). Karena dalam Kasus 1 digunakan uji satu ekor, nilai tersebut harus dibagi dua terlebih dahulu, sehingga pada kasus ini, nilai-p-nya adalah 0,00002831. Karena nilai ini, 0,00002831 < α kita simpulkan penolakan H0.
UJI HIPOTESIS RATA-RATA SATU-SAMPEL DALAM ILMU KOMUNIKASI (1)
Kata “hipotesis” memang jarang ditemukan dalam percakapan sehari-hari. Walaupun demikian, kita sering mendengar kata “dugaan”. Jika suatu hal merupakan suatu dugaan maka hal tersebut belum tentu benar. Untuk mengetahui apakah yang diduga itu benar, kita melakukan penyelidikan. Demikian juga dengan hipotesis. Pada dasarnya, hal yang dihipotesiskan belum tentu benar adanya. Dalam statistika, penyusunan hipotesis perlu ditindaklanjuti dengan penarikan sampel. Jika hasil sampling berhasil membuktikan bahwa hipotesis tersebut keliru maka hipotesis ditolak.
Berikut ini adalah beberapa contoh kasus yang menggambarkan secara sederhana bagaimana uji hipotesis diterapkan dalam ilmu komunikasi.
Kasus 1
Seorang peneliti komunikasi berpendapat bahwa peningkatan waktu yang dihabiskan di media sosial mengakibatkan penurunan keterampilan komunikasi tatap muka di kalangan dewasa muda. Mereka menyusun hipotesis bahwa rata-rata skor keterampilan komunikasi tatap muka (diukur pada skala standar) untuk dewasa muda yang menghabiskan lebih dari 3 jam setiap hari di media sosial lebih rendah daripada skor rata-rata nasional yaitu 75. Berikut adalah sampel yang diambil untuk memeriksa hipotesis tersebut, dalam format .sav: (klik di sini). Pada taraf nyata 0,05, apakah sampel mendukung hipotesis bahwa rata-rata skor lebih rendah dari 75?
Berikut ini akan diuraikan langkah-langkah yang diperlukan untuk menjawab pertanyaan pada Kasus 1.
Langkah 1: Menyusun pasangan hipotesis
H0: μ ≥ 75
H1: μ < 75
Penjelasan Langkah 1
Dalam uji hipotesis statistik, hipotesis dibuat berpasangan, yaitu hipotesis nol (H0) dan hipotesis tandingan/alternatif (H1). Pernyataan dalam H1 adalah pernyataan yang akan dijadikan kesimpulan apabila nanti H0 ditolak. Tanda relasi yang digunakan dalam hipotesis alternatif harus salah satu di antara <, >, atau ≠. Dalam kasus ini, yang akan dibuktikan dalam kasus ini adalah rata-rata skor keterampilan komunikasi tatap muka dewasa muda yang menghabiskan lebih dari 3 jam setiap hari di media sosial lebih rendah daripada skor rata-rata nasional (yaitu 75). Karena itu, pernyataan dalam H1 adalah μ < 75. Relasi yang digunakan dalam H0 adalah sangkalan/ingkaran dari relasi yang digunakan dalam H1. Jadi, pada kasus ini, pernyataan dalam H0 adalah μ ≥ 75.
Langkah 2: Menentukan taraf nyata (α)
Pada kasus ini, taraf nyata telah ditentukan, yaitu sebesar 0,05. Dalam praktik penelitian sesungguhnya, taraf nyata ditentukan oleh peneliti itu sendiri. Taraf nyata adalah peluang terjadinya kesalahan apabila nanti terjadi penolakan hipotesis nol. Dalam kasus ini, jika nanti hipotesis nol ditolak, maka kesimpulannya adalah rata-rata skor keterampilan komunikasi tatap muka dewasa muda yang menghabiskan lebih dari 3 jam setiap hari di media sosial lebih rendah daripada skor rata-rata nasional dan peluang kita salah dalam menyimpulkan ini hanya sebesar 5%.
Langkah 3: Menentukan statistik uji dan daerah penolakan
dengan derajat kebebasan 
. Statistik ini digunakan apabila populasi berdistribusi normal. Dalam teori, terdapat dua statistik lain, yaitu 
dan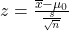 
. Namun, statistik 
jarang digunakan dalam praktik karena dalam praktik,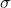 
(simpangan baku populasi) jarang diketahui. (Data pada kasus ini sudah dirancang sedemikian rupa sehingga dapat dianggap bahwa populasi berdistribusi normal, sehingga statistik t dapat digunakan.)
Statistik uji yang digunakan pada kasus ini adalah
Untuk menentukan daerah penolakan, pertama-tama tentukan dulu nilai kritis t-nya. Di salah satu sel lembar Excel, ketikkan: =T.INV(0.05;99). Lihat Gambar 1.
Gambar 1
Setelah tombol Enter ditekan, Excel akan memunculkan nilai -1,660 (apabila dibulatkan hingga 3 tempat desimal). Selanjutnya, daerah penolakan dapat digambarkan sebagai berikut.
Gambar 2
Pada Gambar 2, daerah penolakan ditunjukkan dengan daerah berarsir biru muda. Daerah ini terletak di sisi kiri. Karena itulah uji ini dinamakan uji ekor kiri. Dalam uji ini digunakan ekor kiri karena dalam hipotesis tandingan, digunakan tanda < (lebih kecil dari). Manfaat penentuan daerah penolakan ini adalah untuk memutuskan apakah cukup bukti untuk menolak H0. Apabila nilai t hasil perhitungan (yang diperoleh dari sampel) memiliki nilai kurang dari -1,660 (jatuh di daerah penolakan) maka H0 ditolak.
Langkah 4: Menghitung nilai t dari sampel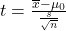
. Tabel berikut menampilkan hasil pengolahan data menggunakan SPSS. (Untuk mengetahui bagaiamana cara menampilkan output SPSS berikut, klik di sini.)
Nilai t dari sampel diperoleh dengan menggunakan rumus
TABEL OUTPUT SPSS
Dari tabel di atas kita mendapatkan nilai t hasil perhitungan (computed t-value, thitung), yaitu sebesar -4,208 dan nilai ini lebih kecil dari nilai kritisnya (yaitu -1,660).
Langkah 5: Penarikan kesimpulan
Nilai thitung pada kasus ini, yaitu -4,208, jatuh di daerah penolakan. Lihat Gambar 3.
Gambar 3
Karena itu, kita menolak hipotesis nol dan selanjutnya menerima hipotesis tandingannya.
KESIMPULAN: Rata-rata skor keterampilan komunikasi tatap muka untuk dewasa muda yang menghabiskan lebih dari 3 jam setiap hari di media sosial secara signifikan lebih rendah daripada skor rata-rata nasional. Peneliti tersebut berhasil mendukung pendapatnya, yaitu bahwa peningkatan waktu yang dihabiskan di media sosial mengakibatkan penurunan keterampilan komunikasi tatap muka di kalangan dewasa muda.
Catatan
Hasil uji hipotesis mungkin signifikan, mungkin juga tidak signifikan. Jika kita berhasil menolak H0 maka uji tersebut dikatakan signifikan dan besarnya peluang terjadi kesalahan dalam penolakan ini adalah sebesar α. Sebaliknya, jika kita gagal menolak H0 maka uji itu dikatakan tidak signifikan. Dalam hal tidak terjadi penolakan H0, besarnya peluang terjadi kesalahan dalam penyimpulan tersebut tidak dapat ditentukan. Dalam Kasus 1, kita berhasil menolak hipotesis nol, sehingga dalam kesimpulannya terdapat frasa “secara signifikan”. Peluang kita salah memberikan kesimpulan ini adalah sebesar taraf nyatanya. Jadi, peluang peneliti tersebut salah menyimpulkan adalah 5%.
CARA LAIN MENARIK KESIMPULAN
Selain menggunakan nilai kritis, terdapat cara lain untuk membuat kesimpulan, yaitu dengan menggunakan nilai-p (p-value). Cara ini kadang-kadang lebih disukai karena cara ini “menghilangkan” Langkah 3 di atas. Dengan cara nilai-p ini, aturan penolakan H0 adalah sebagai berikut: Tolak H0 apabila p < α. Jangan tolak H0 apabila p > α.
Bagaimana menggunakan nilai-p pada Kasus 1? Perhatikan bagian TABEL OUTPUT SPSS di atas yang berjudul One-Sample Test. Di kolom yang berjudul Sig. (2-tailed), terdapat angka 5.662E-005, yaitu 0,00005662. Nilai yang ditunjukkan tersebut merupakan nilai-p untuk uji 2 ekor (2-tailed). Karena dalam Kasus 1 digunakan uji satu ekor, nilai tersebut harus dibagi dua terlebih dahulu, sehingga pada kasus ini, nilai-p-nya adalah 0,00002831. Karena nilai ini, 0,00002831 < α kita simpulkan penolakan H0.
Bagikan ini:
Most visitors also read :
DEKOMPOSISI NILAI SINGULAR (SINGULAR VALUE DECOMPOSITION)
MAXIMUM LIKELIHOOD ESTIMATOR
JARAK STATISTIKAL
SOAL DAN PEMBAHASAN ANALISIS KOMPONEN UTAMA