Kehidupan dipenuhi dengan ketidakpastian. Demikian halnya di bidang logistik, kita dapat menemukan banyak ketidakpastian. Perhatikan variabel-variabel berikut: 1) X1 = banyaknya kesalahan pemenuhan order per hari, 2) X2 = banyaknya pengiriman yang terlambat tiap minggu, 3) X3 = banyaknya kejadian forklift rusak tiap bulan, 4) X4 = alasan keterlambatan pengiriman, 5) X5 = keadaan barang yang tiba di tujuan, 6) X6 = jenis pengemasan, 7) X7 = metode pembayaran. Mari kita lihat nilai-nilai yang mungkin bagi variabel-variabel tersebut.
Perhatikan bahwa untuk keseluruhan variabel tersebut, terdapat ketidakpastian dalam hal nilai yang dimilikinya. Sebagai contoh, tidak ada kepastian mengenai banyaknya kesalahan pemenuhan order tiap harinya (X1). Dalam satu hari tertentu, mungkin tidak terjadi kesalahan, mungkin terjadi hanya 1 kesalahan, mungkin terjadi 2 kesalahan, dan seterusnya. Juga, tidak ada kepastian mengenai keadaan barang yang tiba di tujuan (X5). Suatu barang mungkin tiba di tujuan dalam keadaan rusak, mungkin juga dalam keadaan baik. Walaupun terdapat ketidakpastian dalam semua variabel di atas, variabel-variabel di atas dapat digolongkan ke dalam dua jenis. Variabel X1, X2, dan X3 digolongkan ke dalam variabel acak, sedangkan sisanya bukan variabel acak. Perhatikan bahwa nilai-nilai yang dapat diraih variabel-variabel acak merupakan bilangan nyata, sedangkan nilai-nilai variabel lainnya bukan merupakan bilangan nyata, melainkan nilai-nilai yang berada pada tingkat data nominal.
Erwin Kreyzig, dalam bukunya yang berjudul Advanced Engineering Mathematics (1993) menyatakan bahwa variabel acak atau variabel stokastik adalah suatu fungsi yang terkait dengan suatu eksperimen yang nilai-nilainya merupakan bilangan-bilangan nyata dan kemunculannya bergantung pada peluang. Jadi, pada pokoknya terdapat dua hal esensial yang harus dipenuhi suatu variabel acak.Pertama, nilai-nilai yang mungkin diraihnya merupakan bilangan nyata. Kedua, kemunculan nilai-nilai tersebut bersifat tidak pasti. Contoh lain variabel acak, misalnya: besarnya pendapatan harian suatu toko, lamanya proses bongkar di suatu pelabuhan, banyaknya pengeluaran untuk keperluan iklan suatu perusahaan dalam setahun, banyaknya kuota internet yang dihabiskan mahasiswa tiap bulannya, dan sebagainya.
Variabel acak biasa dilambangkan dengan huruf besar bercetak tebal, misalnya X, Y, Z, dan lain-lain. Besarnya peluang suatu variabel acak X memiliki nilai x dilambangkan dengan P(X = x) atau, apabila konteksnya jelas, dapat disingkat menjadi p(x) Untuk memahami ini, perhatikan contoh berikut.
Contoh
Seorang manajer gudang mempelajari banyaknya kerusakan forklift tiap bulannya (X). Berdasarkan catatan pemeliharaan forklift yang dimilikinya, manajer tersebut telah menetapkan distribusi peluang banyaknya kerusakan tersebut sebagai berikut.
Dari tabel tersebut, kita dapat menuliskan:
P[X = 0] = 0,70
P[X = 1] = 0,20
P[X = 2] = 0,08
P[X = 3] = 0,02
Bagaimana memaknai isi tabel tersebut?
P[X = 0] = 0,70 dapat dibaca “Besarnya peluang tidak terdapat kerusakan dalam satu bulan adalah 70%”.
P[X = 1] = 0,20 dapat dibaca “Besarnya peluang terdapat tepat 1 kerusakan dalam satu bulan adalah 20%”.
P[X = 2] = 0,08 dapat dibaca “Besarnya peluang terdapat tepat 2 kerusakan dalam satu bulan adalah 8%”
P[X = 3] = 0,02 dapat dibaca “Besarnya peluang terdapat tepat 3 kerusakan dalam satu bulan adalah 2%”
Tabel seperti di atas dinamakan tabel distribusi peluang. Selain dalam bentuk tabel, distribusi peluang dapat juga dinyatakan dalam bentuk rumus. Distribusi peluang teoretis pada umumnya dinyatakan dalam bentuk rumus. Beberapa contoh distribusi peluang teoretis adalah distribusi binomial, distribusi Poisson, distribusi hipergeometrik, dan distribusi binomial negatif.
Terhadap variabel acak, kita dapat menghitung rata-rata, variansi, dan simpangan bakunya. Berikut adalah rumus untuk menghitung rata-rata suatu variabel acak diskrit X, yang dilambangkan dengan μX.
.
Variansi variabel acak diskrit X, adalah:
Simpangan bakunya adalah:
Dengan demikian, ketiga ukuran tersebut, apabila dikerjakan dengan bantuan tabel, adalah sebagai berikut.
Selanjutnya,
Kesimpulan
Rata-rata banyaknya kerusakan forklift tiap bulannya adalah 0,42.
Variansi banyaknya kerusakan forklift tiap bulannya adalah 0,52.
Simpangan baku banyaknya kerusakan forklift tiap bulannya adalah 0,72.
VARIABEL ACAK DALAM AKTIVITAS LOGISTIK
Kehidupan dipenuhi dengan ketidakpastian. Demikian halnya di bidang logistik, kita dapat menemukan banyak ketidakpastian. Perhatikan variabel-variabel berikut: 1) X1 = banyaknya kesalahan pemenuhan order per hari, 2) X2 = banyaknya pengiriman yang terlambat tiap minggu, 3) X3 = banyaknya kejadian forklift rusak tiap bulan, 4) X4 = alasan keterlambatan pengiriman, 5) X5 = keadaan barang yang tiba di tujuan, 6) X6 = jenis pengemasan, 7) X7 = metode pembayaran. Mari kita lihat nilai-nilai yang mungkin bagi variabel-variabel tersebut.
Perhatikan bahwa untuk keseluruhan variabel tersebut, terdapat ketidakpastian dalam hal nilai yang dimilikinya. Sebagai contoh, tidak ada kepastian mengenai banyaknya kesalahan pemenuhan order tiap harinya (X1). Dalam satu hari tertentu, mungkin tidak terjadi kesalahan, mungkin terjadi hanya 1 kesalahan, mungkin terjadi 2 kesalahan, dan seterusnya. Juga, tidak ada kepastian mengenai keadaan barang yang tiba di tujuan (X5). Suatu barang mungkin tiba di tujuan dalam keadaan rusak, mungkin juga dalam keadaan baik. Walaupun terdapat ketidakpastian dalam semua variabel di atas, variabel-variabel di atas dapat digolongkan ke dalam dua jenis. Variabel X1, X2, dan X3 digolongkan ke dalam variabel acak, sedangkan sisanya bukan variabel acak. Perhatikan bahwa nilai-nilai yang dapat diraih variabel-variabel acak merupakan bilangan nyata, sedangkan nilai-nilai variabel lainnya bukan merupakan bilangan nyata, melainkan nilai-nilai yang berada pada tingkat data nominal.
Erwin Kreyzig, dalam bukunya yang berjudul Advanced Engineering Mathematics (1993) menyatakan bahwa variabel acak atau variabel stokastik adalah suatu fungsi yang terkait dengan suatu eksperimen yang nilai-nilainya merupakan bilangan-bilangan nyata dan kemunculannya bergantung pada peluang. Jadi, pada pokoknya terdapat dua hal esensial yang harus dipenuhi suatu variabel acak. Pertama, nilai-nilai yang mungkin diraihnya merupakan bilangan nyata. Kedua, kemunculan nilai-nilai tersebut bersifat tidak pasti. Contoh lain variabel acak, misalnya: besarnya pendapatan harian suatu toko, lamanya proses bongkar di suatu pelabuhan, banyaknya pengeluaran untuk keperluan iklan suatu perusahaan dalam setahun, banyaknya kuota internet yang dihabiskan mahasiswa tiap bulannya, dan sebagainya.
Variabel acak biasa dilambangkan dengan huruf besar bercetak tebal, misalnya X, Y, Z, dan lain-lain. Besarnya peluang suatu variabel acak X memiliki nilai x dilambangkan dengan P(X = x) atau, apabila konteksnya jelas, dapat disingkat menjadi p(x) Untuk memahami ini, perhatikan contoh berikut.
Contoh
Seorang manajer gudang mempelajari banyaknya kerusakan forklift tiap bulannya (X). Berdasarkan catatan pemeliharaan forklift yang dimilikinya, manajer tersebut telah menetapkan distribusi peluang banyaknya kerusakan tersebut sebagai berikut.
Dari tabel tersebut, kita dapat menuliskan:
P[X = 0] = 0,70
P[X = 1] = 0,20
P[X = 2] = 0,08
P[X = 3] = 0,02
Bagaimana memaknai isi tabel tersebut?
P[X = 0] = 0,70 dapat dibaca “Besarnya peluang tidak terdapat kerusakan dalam satu bulan adalah 70%”.
P[X = 1] = 0,20 dapat dibaca “Besarnya peluang terdapat tepat 1 kerusakan dalam satu bulan adalah 20%”.
P[X = 2] = 0,08 dapat dibaca “Besarnya peluang terdapat tepat 2 kerusakan dalam satu bulan adalah 8%”
P[X = 3] = 0,02 dapat dibaca “Besarnya peluang terdapat tepat 3 kerusakan dalam satu bulan adalah 2%”
Tabel seperti di atas dinamakan tabel distribusi peluang. Selain dalam bentuk tabel, distribusi peluang dapat juga dinyatakan dalam bentuk rumus. Distribusi peluang teoretis pada umumnya dinyatakan dalam bentuk rumus. Beberapa contoh distribusi peluang teoretis adalah distribusi binomial, distribusi Poisson, distribusi hipergeometrik, dan distribusi binomial negatif.
Terhadap variabel acak, kita dapat menghitung rata-rata, variansi, dan simpangan bakunya. Berikut adalah rumus untuk menghitung rata-rata suatu variabel acak diskrit X, yang dilambangkan dengan μX.
Variansi variabel acak diskrit X,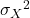
adalah:
![{\sigma_{x}}^2=\sum_{x}^{} (x-\mu_{X})^{2}\cdot P[X=x]](http://edscyclopedia.com/wp-content/ql-cache/quicklatex.com-fdc8a11a8bfbbd96ce4b0b140542d245_l3.png "Rendered by QuickLaTeX.com")
Simpangan bakunya adalah:
Dengan demikian, ketiga ukuran tersebut, apabila dikerjakan dengan bantuan tabel, adalah sebagai berikut.
Selanjutnya,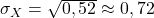
Kesimpulan
Rata-rata banyaknya kerusakan forklift tiap bulannya adalah 0,42.
Variansi banyaknya kerusakan forklift tiap bulannya adalah 0,52.
Simpangan baku banyaknya kerusakan forklift tiap bulannya adalah 0,72.
Bagikan ini:
Most visitors also read :
UJI HIPOTESIS RATA-RATA SATU-SAMPEL DALAM ILMU KOMUNIKASI (2)
UJI HIPOTESIS RATA-RATA SATU-SAMPEL DALAM ILMU KOMUNIKASI (1)
DEKOMPOSISI NILAI SINGULAR (SINGULAR VALUE DECOMPOSITION)
MAXIMUM LIKELIHOOD ESTIMATOR