(English version of this article is available at edsmathscholar.com,click here)
Jika di dalam pembahasan mengenai variabel acak diskrit kita mengenal istilah fungsi peluang atau fungsi massa peluang, maka dalam pembahasan mengenai variabel acak kontinu terdapat istilah fungsi densitas peluang atau disingkat fungsi densitas. Mari kita lihat sebuah definisi.
Definisi fungsi densitas peluang
Fungsi f dikatakan suatu fungsi densitas peluang bagi variabel acak X yang didefinisikan pada himpunan semua bilangan nyata apabila dipenuhi tiga kondisi berikut: 1) untuk setiap , 2) , dan 3) P(a<X<b) = . P(a < X < b) di sini berarti peluang terjadinya a<X<b, yaitu peluang terjadinya nilai X berada di antara a dan b.
Dengan melihat pendefinisian fungsi densitas peluang sebagaimana di atas, tidak lain merupakan luas daerah di bawah kurva f dan di atas sumbu x, yang dibatasi oleh x = a dan x = b. (Lihat Gambar 1.)
Gambar1
Contoh Soal 1
Dalam masa darurat Covid 19, suatu toko hanya boleh beroperasi selama 120 menit, yaitu dari pukul 08:00 hingga 10:00. Calon pembeli tidak boleh berada di dalam toko itu sebelum 08:00 dan wajib meninggalkan toko paling lambat 10:00. Misalkan X adalah variabel acak yang menunjukkan lamanya pelanggan berada di dalam toko, dalam satuan menit. Fungsi densitas peluang dari X diketahui sbb.
Berapakah peluang seorang customer berada di toko: a) antara 10 dan 90 menit, b) antara 30 dan 60 menit? c) kurang dari 20 menit? d) lebih dari 12 menit?
Jawab:
Dengan menggunakan, teknik perhitungan integral tentu:
Dengan mengingat bahwa integral tersebut dapat dipandang sebagai luas daerah di bawah kurva f dan di atas sumbu x, integral pada bagian a adalah luas daerah yang diarsir pada Gambar 2.
Gambar 2
Integral pada bagian a dapat ditentukan dengan menghitung luas persegi panjang berarsir di atas, yaitu dengan panjang = 90 – 10 = 80 dan lebar . Demikian juga bagi integral tentu pada bagian b, integral tersebut dapat dipandang sebagai luas daerah berarsir pada Gambar 3.
Gambar 3
Periksalah bahwa integral pada bagian b di atas (yaitu 0,25) dapat ditentukan dengan cara menghitung luas persegi panjang berarsir pada Gambar 3.
Contoh Soal 2
Dalam suatu pertaruhan, misalkan X adalah banyaknya uang yang dimenangkan, dalam satuan ribu Rupiah. Fungsi densitas dari X diketahui sebagai berikut:
Berapakah peluang seseorang yang mengikuti pertaruhan itu: a) menang lebih dari 2 ribu Rupiah, b) kalah
Jawab:
Fungsi densitas peluang bagi X dapat digambarkan sbb.
Gambar 4
Untuk menjawab pertanyaan a, kita hitung luas daerah segitiga pada Gambar 5 berikut.
Gambar 5
Alas segitiga itu adalah 4 – 2 = 2. Tinggi segitiga adalah f(2) = 0,08 – (0,02).2 = 0,04. Jadi, luas segitiga itu adalah .
Jadi, peluang orang tersebut menang lebih dari Rp 2 ribu adalah 0,04.
Cara lain adalah dengan menggunakan integral tentu sebagai berikut.
(sama dengan perhitungan menggunakan luas daerah)
Untuk menjawab pertanyaan b, kita dapat menghitung luas daerah trapesium pada Gambar 6.
Gambar 6
Perhatikan bahwa panjang AD = 0,2, panjang BC = 0,08, AB = 6, sehingga luas trapesium ABCD adalah
Apabila akan digunakan integral tentu, soal bagian b ini dikerjakan sebagai berikut.
FUNGSI DENSITAS PELUANG
(English version of this article is available at edsmathscholar.com, click here)
Jika di dalam pembahasan mengenai variabel acak diskrit kita mengenal istilah fungsi peluang atau fungsi massa peluang, maka dalam pembahasan mengenai variabel acak kontinu terdapat istilah fungsi densitas peluang atau disingkat fungsi densitas. Mari kita lihat sebuah definisi.
Definisi fungsi densitas peluang apabila dipenuhi tiga kondisi berikut: 1)
apabila dipenuhi tiga kondisi berikut: 1)  untuk setiap
untuk setiap  , 2)
, 2)  , dan 3) P(a<X<b) =
, dan 3) P(a<X<b) = 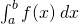 . P(a < X < b) di sini berarti peluang terjadinya a<X<b, yaitu peluang terjadinya nilai X berada di antara a dan b.
. P(a < X < b) di sini berarti peluang terjadinya a<X<b, yaitu peluang terjadinya nilai X berada di antara a dan b.
Fungsi f dikatakan suatu fungsi densitas peluang bagi variabel acak X yang didefinisikan pada himpunan semua bilangan nyata
Dengan melihat pendefinisian fungsi densitas peluang sebagaimana di atas, tidak lain merupakan luas daerah di bawah kurva f dan di atas sumbu x, yang dibatasi oleh x = a dan x = b. (Lihat Gambar 1.)
tidak lain merupakan luas daerah di bawah kurva f dan di atas sumbu x, yang dibatasi oleh x = a dan x = b. (Lihat Gambar 1.)
Gambar 1
Contoh Soal 1
Dalam masa darurat Covid 19, suatu toko hanya boleh beroperasi selama 120 menit, yaitu dari pukul 08:00 hingga 10:00. Calon pembeli tidak boleh berada di dalam toko itu sebelum 08:00 dan wajib meninggalkan toko paling lambat 10:00. Misalkan X adalah variabel acak yang menunjukkan lamanya pelanggan berada di dalam toko, dalam satuan menit. Fungsi densitas peluang dari X diketahui sbb.
Berapakah peluang seorang customer berada di toko: a) antara 10 dan 90 menit, b) antara 30 dan 60 menit? c) kurang dari 20 menit? d) lebih dari 12 menit?
Jawab:
Dengan menggunakan, teknik perhitungan integral tentu:
Dengan mengingat bahwa integral tersebut dapat dipandang sebagai luas daerah di bawah kurva f dan di atas sumbu x, integral pada bagian a adalah luas daerah yang diarsir pada Gambar 2.
Gambar 2
Integral pada bagian a dapat ditentukan dengan menghitung luas persegi panjang berarsir di atas, yaitu dengan panjang = 90 – 10 = 80 dan lebar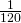 . Demikian juga bagi integral tentu pada bagian b, integral tersebut dapat dipandang sebagai luas daerah berarsir pada Gambar 3.
. Demikian juga bagi integral tentu pada bagian b, integral tersebut dapat dipandang sebagai luas daerah berarsir pada Gambar 3.
Gambar 3
Periksalah bahwa integral pada bagian b di atas (yaitu 0,25) dapat ditentukan dengan cara menghitung luas persegi panjang berarsir pada Gambar 3.
Contoh Soal 2
Dalam suatu pertaruhan, misalkan X adalah banyaknya uang yang dimenangkan, dalam satuan ribu Rupiah. Fungsi densitas dari X diketahui sebagai berikut:
Berapakah peluang seseorang yang mengikuti pertaruhan itu: a) menang lebih dari 2 ribu Rupiah, b) kalah
Jawab:
Fungsi densitas peluang bagi X dapat digambarkan sbb.
Gambar 4
Untuk menjawab pertanyaan a, kita hitung luas daerah segitiga pada Gambar 5 berikut.
Gambar 5
Alas segitiga itu adalah 4 – 2 = 2. Tinggi segitiga adalah f(2) = 0,08 – (0,02).2 = 0,04. Jadi, luas segitiga itu adalah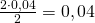 .
.
Jadi, peluang orang tersebut menang lebih dari Rp 2 ribu adalah 0,04.
Cara lain adalah dengan menggunakan integral tentu sebagai berikut.
(sama dengan perhitungan menggunakan luas daerah)
Untuk menjawab pertanyaan b, kita dapat menghitung luas daerah trapesium pada Gambar 6.
Gambar 6
Perhatikan bahwa panjang AD = 0,2, panjang BC = 0,08, AB = 6, sehingga luas trapesium ABCD adalah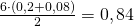
Apabila akan digunakan integral tentu, soal bagian b ini dikerjakan sebagai berikut.
(sama dengan perhitungan menggunakan luas daerah)
LATIHAN SOAL
Latihan 1
Bagikan ini:
Most visitors also read :
DEKOMPOSISI NILAI SINGULAR (SINGULAR VALUE DECOMPOSITION)
MAXIMUM LIKELIHOOD ESTIMATOR
JARAK STATISTIKAL
SOAL DAN PEMBAHASAN ANALISIS KOMPONEN UTAMA