DALIL LIMIT PUSAT DALAM DISTRIBUSI SAMPLING RATA-RATA
Pebruari 26th, 2020
Di bagian lalu telah dibahas bagaimana distribusi sampling rata-rata untuk suatu populasi yang anggota-anggotanya diketahui. Pada contoh yang disajikan, populasi yang diamati terdiri dari 5 buah anggota, yaitu 78, 60, 60, 54, dan 48. Apabila dilakukan sampling tanpa pengembalian dengan ukuran 3, akan diperoleh distribusi sampling rata-rata sebagai berikut.
Sedangkan apabila sampel yang diambil berukuran 2 (tanpa pengembalian) akan diperoleh distribusi sampling rata-rata sebagai berikut.
Sebagaimana telah dibahas pada artikel sebelumnya, dalam penerapan statistika sesungguhnya, ukuran populasi biasanya sangat banyak, bahkan tak berhingga. Bagaimana distribusi sampling rata-rata apabila sampel dengan ukuran tertentu diambil populasi tersebut? Pembahasannya kita bedakan menjadi dua bagian, yaitu apabila populasi asal sampel tersebut berdistribusi normal dan apabila sampel tersebut diambil dari sembarang populasi.
BAGIAN I: SAMPEL DIAMBIL DARI POPULASI BERDISTRIBUSI NORMAL
Jika sampel berukuran n diambil dari populasi yang berdistribusi normal dengan rata-rata dan simpangan baku , maka distribusi sampling dari rata-rata akan berdistribusi normal dengan rata-rata dan simpangan baku . Perlu digarisbawahi bahwa pernyataan tersebut berlaku untuk sembarang ukuran sampel n = 1, 2, 3, …
Sebagai ilustrasi, misalnya lamanya waktu menunggu di suatu restoran berdistribusi normal dengan rata-rata 240 detik dengan simpangan baku 5 detik. Misalkan ukuran sampel yang digunakan adalah 4 (yaitu, n = 4). Seandainya sampling berukuran 4 tersebut diulang-ulang cukup banyak, maka rata-rata sampel yang diraih akan beragam; dengan kata lain akan terbentuk distribusi sampling rata-rata. Dengan bantuan software statistika yang bernama R, diperoleh distribusi sampling rata-rata sebagai berikut.
Dari populasi yang sama, seandainya digunakan hanya 2 buah sampel, akan diperoleh distribusi sampling rata-rata sebagai berikut.
Seperti dapat dilihat pada histogram-histogram di atas, distribusi sampling dari rata-rata tampak berdistribusi normal.
Contoh 1
Lamanya seorang pegawai teller di suatu bank menghabiskan waktu dengan pelanggan diketahui berdistribusi normal dengan rata-rata 200 detik dan simpangan baku 15 detik. Jika kemudian akan diambil 9 sampel pengukuran lamanya waktu tersebut, berapa peluangnya diperoleh rata-rata sampel antara 195 detik dan 208 detik?
Jawab
Pada soal ini, dan . Karena sampel diambil dari populasi yang berdistribusi normal, maka distribusi sampling rata-ratanya juga akan berdistribusi normal dengan rata-rata dan simpangan baku . Yang ditanyakan adalah . Peluang tersebut diperoleh dengan menghitung luas daerah di bawah kurva normal sebagai berikut.
Dengan menggunakan tabel luas daerah di bawah kurva normal baku, diperoleh p = 0,3413+0,4452 = 0,7865. Jadi, kita akan mendapat rata-rata sampel antara 195 detik dan 208 detik dengan peluang 78,65%.
Contoh 2
Pada Contoh 1, berapa peluang kita akan mendapatkan sampel yang rata-ratanya lebih dari 206 detik?
Jawab
Yang ditanyakan adalah . Peluang tersebut diperoleh dengan menghitung luas daerah di bawah kurva normal sebagai berikut.
Dengan menggunakan tabel luas daerah di bawah kurva normal baku, diperoleh p = 0,5 – 0,3849 = 0,1151. Jadi, kita akan mendapat rata-rata sampel lebih dari 206 detik dengan peluang 11,51%.
BAGIAN II: SAMPEL DIAMBIL DARI POPULASI BERDISTRIBUSI TAK DIKETAHUI ATAU BUKAN NORMAL
Ada kalanya kita tidak mengetahui apakah populasi yang dihadapi berdistribusi normal atau tidak. Beruntungnya, ada suatu dalil/teorema yang luar biasa pentingnya dalam statistika, yaitu Central Limit Theorem (Dalil Limit Pusat) sebagai berikut.
Jika adalah rata-rata suatu sampel acak berukuran n yang diambil dari suatu populasi dengan rata-rata dan simpangan baku terhingga , maka distribusi dari menuju distribusi normal baku apabila .
Dengan kata lain, untuk ukuran sampel yang cukup besar, distribusi sampling rata-rata menuju (semakin mendekati) distribusi normal. Hal ini berlaku untuk sampel yang diambil dari populasi berdistribusi apa pun, selama simpangan bakunya berhingga. Dalam kebanyakan praktik, ukuran sampel yang cukup besar di sini adalah 30 atau lebih.
Contoh 3
Rata-rata biaya per tahun yang dikeluarkan untuk keperluan iklan oleh perusahaan-perusahaan yang bergerak di industri tertentu adalah Rp 200 juta dengan simpangan baku Rp 12 juta. Apabila secara acak diambil sampel berukuran 36 dari perusahaan-perusahaan di industri tersebut, berapakah peluang diperoleh rata-rata sampel kurang dari Rp 195 juta?
Jawab
Dalam kasus ini distribusi biaya tahunan untuk iklan tidak diketahui. Namun karena ukuran sampelnya tidak kurang dari 30, dalil limit pusat memperbolehkan kita menerapkan cara serupa contoh-contoh sebelumnya di atas. Pada soal ini, dan . Rata-rata dari distribusi sampling rata-rata dan simpangan bakunya . Yang ditanyakan adalah . Peluang tersebut diperoleh dengan menghitung luas daerah di bawah kurva normal sebagai berikut.
Dengan menggunakan tabel luas daerah di bawah kurva normal baku, diperoleh p = 0,5 – 0,4938 = 0,0062. Jadi, kita akan mendapat rata-rata sampel kurang dari Rp 195 juta dengan peluang 0,62%.
Lengkapi pemahaman Anda mengenai materi ini di youtube channel kami: (klik di sini)
LATIHAN
Soal 1
IPK seluruh alumni Tel-U diketahui berdistribusi normal dengan rata-rata 3,10 dan simpangan baku 0,2. Kemudian akan diambil 16 orang alumni Tel-U sebagai sampel untuk selanjutnya dihitung rata-rata sampelnya. Berapa peluang rata-rata sampel itu lebih dari 3,25?
Soal 2
Lamanya waktu menunggu lulusan sebuah perguruan tinggi sejak waktu kelulusan hingga mendapat pekerjaan memiliki rata-rata 250 hari dan simpangan baku 20 hari. Apabila akan diambil sampel 80 orang dari populasi tersebut, berapa peluang diperoleh rata-rata waktu menunggu antara 245 hari dan 252 hari?
DALIL LIMIT PUSAT DALAM DISTRIBUSI SAMPLING RATA-RATA
Di bagian lalu telah dibahas bagaimana distribusi sampling rata-rata untuk suatu populasi yang anggota-anggotanya diketahui. Pada contoh yang disajikan, populasi yang diamati terdiri dari 5 buah anggota, yaitu 78, 60, 60, 54, dan 48. Apabila dilakukan sampling tanpa pengembalian dengan ukuran 3, akan diperoleh distribusi sampling rata-rata sebagai berikut.
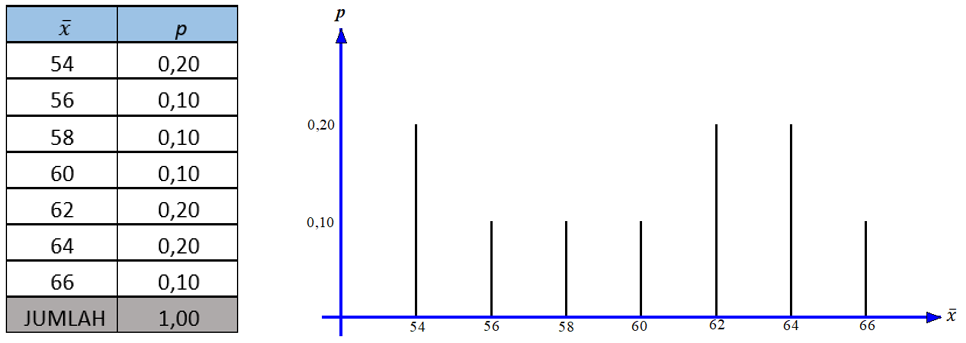
Sedangkan apabila sampel yang diambil berukuran 2 (tanpa pengembalian) akan diperoleh distribusi sampling rata-rata sebagai berikut.
Sebagaimana telah dibahas pada artikel sebelumnya, dalam penerapan statistika sesungguhnya, ukuran populasi biasanya sangat banyak, bahkan tak berhingga. Bagaimana distribusi sampling rata-rata apabila sampel dengan ukuran tertentu diambil populasi tersebut? Pembahasannya kita bedakan menjadi dua bagian, yaitu apabila populasi asal sampel tersebut berdistribusi normal dan apabila sampel tersebut diambil dari sembarang populasi.
BAGIAN I: SAMPEL DIAMBIL DARI POPULASI BERDISTRIBUSI NORMAL
Jika sampel berukuran n diambil dari populasi yang berdistribusi normal dengan rata-rata
dan simpangan baku 
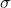, maka distribusi sampling dari rata-rata 
akan berdistribusi normal dengan rata-rata 
dan simpangan baku 
. Perlu digarisbawahi bahwa pernyataan tersebut berlaku untuk sembarang ukuran sampel n = 1, 2, 3, …
Sebagai ilustrasi, misalnya lamanya waktu menunggu di suatu restoran berdistribusi normal dengan rata-rata 240 detik dengan simpangan baku 5 detik. Misalkan ukuran sampel yang digunakan adalah 4 (yaitu, n = 4). Seandainya sampling berukuran 4 tersebut diulang-ulang cukup banyak, maka rata-rata sampel yang diraih akan beragam; dengan kata lain akan terbentuk distribusi sampling rata-rata. Dengan bantuan software statistika yang bernama R, diperoleh distribusi sampling rata-rata sebagai berikut.
Dari populasi yang sama, seandainya digunakan hanya 2 buah sampel, akan diperoleh distribusi sampling rata-rata sebagai berikut.
Seperti dapat dilihat pada histogram-histogram di atas, distribusi sampling dari rata-rata tampak berdistribusi normal.
Contoh 1
Lamanya seorang pegawai teller di suatu bank menghabiskan waktu dengan pelanggan diketahui berdistribusi normal dengan rata-rata 200 detik dan simpangan baku 15 detik. Jika kemudian akan diambil 9 sampel pengukuran lamanya waktu tersebut, berapa peluangnya diperoleh rata-rata sampel antara 195 detik dan 208 detik?
Jawab
dan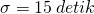 
. Karena sampel diambil dari populasi yang berdistribusi normal, maka distribusi sampling rata-ratanya juga akan berdistribusi normal dengan rata-rata 
dan simpangan baku 
. Yang ditanyakan adalah ![p = P[195 \: detik < \bar{X} < 208 \: detik]](http://edscyclopedia.com/wp-content/ql-cache/quicklatex.com-5552b7d5a4ffdbeb3b97bd3919b45e5e_l3.png "Rendered by QuickLaTeX.com")
. Peluang tersebut diperoleh dengan menghitung luas daerah di bawah kurva normal sebagai berikut.
Pada soal ini,
Dengan menggunakan tabel luas daerah di bawah kurva normal baku, diperoleh p = 0,3413+0,4452 = 0,7865. Jadi, kita akan mendapat rata-rata sampel antara 195 detik dan 208 detik dengan peluang 78,65%.
Contoh 2
Pada Contoh 1, berapa peluang kita akan mendapatkan sampel yang rata-ratanya lebih dari 206 detik?
Jawab![p = P[\bar{X} > 206 \: detik]](http://edscyclopedia.com/wp-content/ql-cache/quicklatex.com-ea1b23123523bed9493c0a76c1ba3132_l3.png "Rendered by QuickLaTeX.com")
. Peluang tersebut diperoleh dengan menghitung luas daerah di bawah kurva normal sebagai berikut.
Yang ditanyakan adalah
Dengan menggunakan tabel luas daerah di bawah kurva normal baku, diperoleh p = 0,5 – 0,3849 = 0,1151. Jadi, kita akan mendapat rata-rata sampel lebih dari 206 detik dengan peluang 11,51%.
BAGIAN II: SAMPEL DIAMBIL DARI POPULASI BERDISTRIBUSI TAK DIKETAHUI ATAU BUKAN NORMAL
Ada kalanya kita tidak mengetahui apakah populasi yang dihadapi berdistribusi normal atau tidak. Beruntungnya, ada suatu dalil/teorema yang luar biasa pentingnya dalam statistika, yaitu Central Limit Theorem (Dalil Limit Pusat) sebagai berikut.
Jika
adalah rata-rata suatu sampel acak berukuran n yang diambil dari suatu populasi dengan rata-rata 
dan simpangan baku terhingga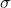 
, maka distribusi dari 
menuju distribusi normal baku apabila 
.
Dengan kata lain, untuk ukuran sampel yang cukup besar, distribusi sampling rata-rata menuju (semakin mendekati) distribusi normal. Hal ini berlaku untuk sampel yang diambil dari populasi berdistribusi apa pun, selama simpangan bakunya berhingga. Dalam kebanyakan praktik, ukuran sampel yang cukup besar di sini adalah 30 atau lebih.
Contoh 3
Rata-rata biaya per tahun yang dikeluarkan untuk keperluan iklan oleh perusahaan-perusahaan yang bergerak di industri tertentu adalah Rp 200 juta dengan simpangan baku Rp 12 juta. Apabila secara acak diambil sampel berukuran 36 dari perusahaan-perusahaan di industri tersebut, berapakah peluang diperoleh rata-rata sampel kurang dari Rp 195 juta?
Jawab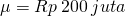
dan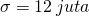 
. Rata-rata dari distribusi sampling rata-rata 
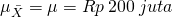dan simpangan bakunya 
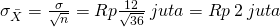. Yang ditanyakan adalah ![p = P[\bar{X} < Rp \: 195 \: juta]](http://edscyclopedia.com/wp-content/ql-cache/quicklatex.com-5f73a2f0e286e7dcde8f13fd1bf9cd10_l3.png "Rendered by QuickLaTeX.com")
. Peluang tersebut diperoleh dengan menghitung luas daerah di bawah kurva normal sebagai berikut.
Dalam kasus ini distribusi biaya tahunan untuk iklan tidak diketahui. Namun karena ukuran sampelnya tidak kurang dari 30, dalil limit pusat memperbolehkan kita menerapkan cara serupa contoh-contoh sebelumnya di atas. Pada soal ini,
Dengan menggunakan tabel luas daerah di bawah kurva normal baku, diperoleh p = 0,5 – 0,4938 = 0,0062. Jadi, kita akan mendapat rata-rata sampel kurang dari Rp 195 juta dengan peluang 0,62%.
Lengkapi pemahaman Anda mengenai materi ini di youtube channel kami: (klik di sini)
LATIHAN
Soal 1
IPK seluruh alumni Tel-U diketahui berdistribusi normal dengan rata-rata 3,10 dan simpangan baku 0,2. Kemudian akan diambil 16 orang alumni Tel-U sebagai sampel untuk selanjutnya dihitung rata-rata sampelnya. Berapa peluang rata-rata sampel itu lebih dari 3,25?
Soal 2
Lamanya waktu menunggu lulusan sebuah perguruan tinggi sejak waktu kelulusan hingga mendapat pekerjaan memiliki rata-rata 250 hari dan simpangan baku 20 hari. Apabila akan diambil sampel 80 orang dari populasi tersebut, berapa peluang diperoleh rata-rata waktu menunggu antara 245 hari dan 252 hari?
Bagikan ini:
Most visitors also read :
DEKOMPOSISI NILAI SINGULAR (SINGULAR VALUE DECOMPOSITION)
MAXIMUM LIKELIHOOD ESTIMATOR
JARAK STATISTIKAL
SOAL DAN PEMBAHASAN ANALISIS KOMPONEN UTAMA