Penelitian-penelitian dalam ilmu komunikasi sering menguji apakah suatu variabel berpengaruh terhadap variabel lainnya. Misalnya: 1) Apakah jumlah unggahan media sosial memengaruhi keterlibatan audiens? 2) Apakah panjang pesan memengaruhi kemampuan pendengar untuk mengingatnya? 3) Apakah kredibilitas juru bicara berpengaruh terhadap kemampuan persuasi? Untuk menjawab atau menguji hal-hal tersebut, kita dapat menggunakan model-model regresi dalam statistika. Model regresi yang paling sederhana dalam statistika adalah regresi linier sederhana.
Regresi linier sederhana memberikan setidaknya dua kegunaan, yaitu untuk menguji pengaruh suatu variabel terhadap variabel lain, dan meramalkan nilai salah satu variabel berdasarkan nilai variabel lainnya. Variabel yang diduga dipengaruhi dinamakan variabel terikat atau variabel yang dijelaskan, sedangkan variabel yang diduga memengaruhi dinamakan variabel bebas atau variabel penjelas (explanatory variable).
Dalam regresi linier sederhana, diasumsikan bahwa hubungan antara variabel terikat (misalnya Y) dengan variabel bebasnya (misalnya X) dinyatakan dalam fungsi regresi populasi (population regression function, PRF) sebagai berikut: E(Y|X) = β0 + β1X. Pada persamaan tersebut, β0 dinamakan intercept dan β1 dinamakan slope. E(Y|X) adalah rata-rata nilai Y apabila X memiliki nilai tertentu. Sebagai contoh, misalnya Y menyatakan pengeluaran per bulan (dalam juta Rupiah), X menyatakan pendapatan per bulan (dalam juta Rupiah), dan persamaan regresi populasinya adalah E(Y|X) = 2 + 0,3X. Jika pendapatan keluarga adalah Rp 10 juta per bulan maka rata-rata pengeluaran keluarga itu adalah Rp 5 juta per bulan. [Perhatikan: Y = 2 + (0,3 x 10) = 5]. Tetapi tidak semua keluarga yang berpenghasilan Rp 10 juta per bulan menghabiskan Rp 5 juta per bulan. Untuk masing-masing keluarga, misalkan keluarga ke-i (yang berpenghasilan X), besarnya pengeluaran adalah Yi = 2 + 0,3X + ui. Dalam persamaan di atas, ui dinamakan stochastic disturbance atau error term. Nilai ini mengukur penyimpangan nilai aktual Y terhadap rata-ratanya. Dalam contoh ini, jika sebuah keluarga pendapatannya Rp 10 juta per bulan dan pengeluarannya adalah Rp 7 juta per bulan, maka untuk keluarga ini, u = Rp 2 juta per bulan. Tetapi, untuk keluarga lain yang pendapatannya sama sebesar Rp 10 juta per bulan dan pengeluarannya Rp 4 juta per bulan, maka untuk keluarga tersebut, u = – Rp 1 juta. Jadi, nilai u berbeda untuk setiap keluarga pada tingkat pendapatan yang sama. Dalam regresi linier sederhana, diasumsikan bahwa ui berdistribusi normal dengan rata-rata nol.
Pengujian adanya pengaruh suatu variabel terhadap variabel yang lain merupakan suatu hal yang penting. Apabila pengaruh tersebut signifikan, kita dapat merekayasa nilai variabel terikat dengan merekayasa atau mengubah nilai variabel penjelas. Misalkan panjangnya siaran pers secara signifikan memengaruhi banyaknya liputan media. Dengan adanya pengaruh tersebut, kita dapat memperbanyak liputan media dengan cara mengubah panjangnya siaran pers.
UJI SIGNIFIKANSI PENGARUH
Dalam pengujian ini, terdapat dua persamaan penting yang terlibat, yaitu population regression function (PRF) dan sample regression function (SRF).
PRF dalam bentuk stokastik:
SRF dalam bentuk stokastik:
Kita tak dapat mengetahui nilai sesungguhnya dari koefisien-koefisien beta dalam PRF. Nilai-nilai tersebut hanya bisa ditaksir menggunakan koefisien-koefisien beta dalam SRF. Nilai-nilai tersebut diperoleh dengan mengolah hasil sampling. Dengan bantuan perangkat lunak, seperti SPSS, kita akan mendapatkan nilai dan .
Berikut ini adalah langkah-langkah uji hipotesis untuk memeriksa adanya pengaruh.
H0: β1 = 0 [X tidak berpengaruh terhadap Y.]
H1: β1 ≠ 0 [X berpengaruh terhadap Y.]
Taraf nyata: α = 0,05
Statistik uji: dengan derajat kebebasan ν = n – 2 dan adalah standard error dari .
Kriteria penolakan H0: Tolak H0 apabila nilai-p < α.
Hitung/dapatkan nilai t dari sampel dan nilai-p-nya, kemudian berikan keputusan berdasarkan kriteria di atas.
CONTOH
Seorang pemimpin perusahaan sedang mempertimbangkan apakah diperlukan tambahan anggaran untuk biaya promosi sejenis produk agar penjualan (sales) produk itu meningkat. Untuk itu ia mengambil sampel sales dan biaya promosi (dalam juta Rupiah) di 10 daerah pemasaran produk itu, dan diperoleh hasil sebagai berikut.
Pada taraf nyata 0,05 apakah terdapat pengaruh promosi terhadap sales?
Jawab
Misalkan X = biaya promosi dan Y = sales.
PRF:
SRF:
H0: β1 = 0 [Promosi tidak berpengaruh terhadap sales.]
H1: β1 ≠ 0 [Promosi berpengaruh terhadap sales.]
Taraf nyata: α = 0,05
Statistik uji: dengan derajat kebebasan ν = n – 2
Kriteria penolakan H0: Tolak H0 apabila nilai-p < 0,05.
Hasil pengolahan data menggunakan SPSS:
Dari tabel di atas, diperoleh hal-hal sebagai berikut.
Jadi, fungsi regresi sampelnya adalah
Nilai-p untuk biaya promosi adalah 0,006 < 0,05.
Karena nilai-p < α, tolak H0.
Jadi, promosi secara signifikan berpengaruh terhadap sales.
SOAL
Bagaimana hubungan antara jumlah pengeluaran yang dihabiskan per minggu untuk rekreasi dan jumlah anggota keluarga? Apakah keluarga yang lebih besar menghabiskan lebih banyak uang untuk rekreasi? Sampel dari 10 keluarga di wilayah Chicago menunjukkan angka-angka berikut untuk jumlah anggota keluarga dan jumlah yang dihabiskan untuk rekreasi per minggu.
Dapatkah kita simpulkan bahwa jumlah anggota keluarga berpengaruh searah terhadap jumlah yang dihabiskan untuk rekreasi? Catatan: “searah” di sini berarti bahwa semakin banyak anggota keluarga berdampak pada semakin banyaknya pengeluaran untuk rekreasi.
BERKENALAN DENGAN REGRESI LINIER SEDERHANA
Penelitian-penelitian dalam ilmu komunikasi sering menguji apakah suatu variabel berpengaruh terhadap variabel lainnya. Misalnya: 1) Apakah jumlah unggahan media sosial memengaruhi keterlibatan audiens? 2) Apakah panjang pesan memengaruhi kemampuan pendengar untuk mengingatnya? 3) Apakah kredibilitas juru bicara berpengaruh terhadap kemampuan persuasi? Untuk menjawab atau menguji hal-hal tersebut, kita dapat menggunakan model-model regresi dalam statistika. Model regresi yang paling sederhana dalam statistika adalah regresi linier sederhana.
Regresi linier sederhana memberikan setidaknya dua kegunaan, yaitu untuk menguji pengaruh suatu variabel terhadap variabel lain, dan meramalkan nilai salah satu variabel berdasarkan nilai variabel lainnya. Variabel yang diduga dipengaruhi dinamakan variabel terikat atau variabel yang dijelaskan, sedangkan variabel yang diduga memengaruhi dinamakan variabel bebas atau variabel penjelas (explanatory variable).
Dalam regresi linier sederhana, diasumsikan bahwa hubungan antara variabel terikat (misalnya Y) dengan variabel bebasnya (misalnya X) dinyatakan dalam fungsi regresi populasi (population regression function, PRF) sebagai berikut: E(Y|X) = β0 + β1X. Pada persamaan tersebut, β0 dinamakan intercept dan β1 dinamakan slope. E(Y|X) adalah rata-rata nilai Y apabila X memiliki nilai tertentu. Sebagai contoh, misalnya Y menyatakan pengeluaran per bulan (dalam juta Rupiah), X menyatakan pendapatan per bulan (dalam juta Rupiah), dan persamaan regresi populasinya adalah E(Y|X) = 2 + 0,3X. Jika pendapatan keluarga adalah Rp 10 juta per bulan maka rata-rata pengeluaran keluarga itu adalah Rp 5 juta per bulan. [Perhatikan: Y = 2 + (0,3 x 10) = 5]. Tetapi tidak semua keluarga yang berpenghasilan Rp 10 juta per bulan menghabiskan Rp 5 juta per bulan. Untuk masing-masing keluarga, misalkan keluarga ke-i (yang berpenghasilan X), besarnya pengeluaran adalah Yi = 2 + 0,3X + ui. Dalam persamaan di atas, ui dinamakan stochastic disturbance atau error term. Nilai ini mengukur penyimpangan nilai aktual Y terhadap rata-ratanya. Dalam contoh ini, jika sebuah keluarga pendapatannya Rp 10 juta per bulan dan pengeluarannya adalah Rp 7 juta per bulan, maka untuk keluarga ini, u = Rp 2 juta per bulan. Tetapi, untuk keluarga lain yang pendapatannya sama sebesar Rp 10 juta per bulan dan pengeluarannya Rp 4 juta per bulan, maka untuk keluarga tersebut, u = – Rp 1 juta. Jadi, nilai u berbeda untuk setiap keluarga pada tingkat pendapatan yang sama. Dalam regresi linier sederhana, diasumsikan bahwa ui berdistribusi normal dengan rata-rata nol.
Pengujian adanya pengaruh suatu variabel terhadap variabel yang lain merupakan suatu hal yang penting. Apabila pengaruh tersebut signifikan, kita dapat merekayasa nilai variabel terikat dengan merekayasa atau mengubah nilai variabel penjelas. Misalkan panjangnya siaran pers secara signifikan memengaruhi banyaknya liputan media. Dengan adanya pengaruh tersebut, kita dapat memperbanyak liputan media dengan cara mengubah panjangnya siaran pers.
UJI SIGNIFIKANSI PENGARUH
Dalam pengujian ini, terdapat dua persamaan penting yang terlibat, yaitu population regression function (PRF) dan sample regression function (SRF).
PRF dalam bentuk stokastik: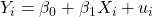
SRF dalam bentuk stokastik: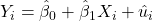
Kita tak dapat mengetahui nilai sesungguhnya dari koefisien-koefisien beta dalam PRF. Nilai-nilai tersebut hanya bisa ditaksir menggunakan koefisien-koefisien beta dalam SRF. Nilai-nilai tersebut diperoleh dengan mengolah hasil sampling. Dengan bantuan perangkat lunak, seperti SPSS, kita akan mendapatkan nilai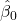
dan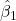 
.
Berikut ini adalah langkah-langkah uji hipotesis untuk memeriksa adanya pengaruh.
H0: β1 = 0 [X tidak berpengaruh terhadap Y.]
H1: β1 ≠ 0 [X berpengaruh terhadap Y.]
Taraf nyata: α = 0,05
Statistik uji: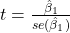
dengan derajat kebebasan ν = n – 2 dan 
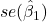adalah standard error dari 
.
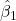Kriteria penolakan H0: Tolak H0 apabila nilai-p < α.
Hitung/dapatkan nilai t dari sampel dan nilai-p-nya, kemudian berikan keputusan berdasarkan kriteria di atas.
CONTOH
Seorang pemimpin perusahaan sedang mempertimbangkan apakah diperlukan tambahan anggaran untuk biaya promosi sejenis produk agar penjualan (sales) produk itu meningkat. Untuk itu ia mengambil sampel sales dan biaya promosi (dalam juta Rupiah) di 10 daerah pemasaran produk itu, dan diperoleh hasil sebagai berikut.
Pada taraf nyata 0,05 apakah terdapat pengaruh promosi terhadap sales?
Jawab
Misalkan X = biaya promosi dan Y = sales.
PRF: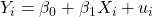
SRF: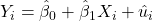
H0: β1 = 0 [Promosi tidak berpengaruh terhadap sales.]
H1: β1 ≠ 0 [Promosi berpengaruh terhadap sales.]
Taraf nyata: α = 0,05
Statistik uji: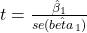
dengan derajat kebebasan ν = n – 2
Kriteria penolakan H0: Tolak H0 apabila nilai-p < 0,05.
Hasil pengolahan data menggunakan SPSS:
Dari tabel di atas, diperoleh hal-hal sebagai berikut.
Jadi, fungsi regresi sampelnya adalah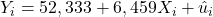
Nilai-p untuk biaya promosi adalah 0,006 < 0,05.
Karena nilai-p < α, tolak H0.
Jadi, promosi secara signifikan berpengaruh terhadap sales.
SOAL
Bagaimana hubungan antara jumlah pengeluaran yang dihabiskan per minggu untuk rekreasi dan jumlah anggota keluarga? Apakah keluarga yang lebih besar menghabiskan lebih banyak uang untuk rekreasi? Sampel dari 10 keluarga di wilayah Chicago menunjukkan angka-angka berikut untuk jumlah anggota keluarga dan jumlah yang dihabiskan untuk rekreasi per minggu.
Dapatkah kita simpulkan bahwa jumlah anggota keluarga berpengaruh searah terhadap jumlah yang dihabiskan untuk rekreasi? Catatan: “searah” di sini berarti bahwa semakin banyak anggota keluarga berdampak pada semakin banyaknya pengeluaran untuk rekreasi.
Bagikan ini:
Most visitors also read :
PENGUJIAN VALIDITAS KUESIONER DENGAN CARA SEDERHANA
PENDAHULUAN REGRESI LINIER BERGANDA
BERKENALAN DENGAN DISTRIBUSI NORMAL BAKU
KOEFISIEN KORELASI SPEARMAN’S RHO