(English version of this article is available at edsmathscholar.com,click here)
Salah satu hal yang perlu dipahami untuk mempelajari statistika multivariat adalah matriks varians-kovarians. Statistika multivariat berhubungan dengan n x p buah data hasil sampling, di mana n adalah banyaknya sampel dan p adalah banyaknya pengukuran yang dilakukan terhadap masing-masing sampel. Sebagai contoh, dilakukan pengukuran terhadap 4 orang sampel penelitian. Kepada setiap sampel tersebut ditanyakan tiga hal, yaitu: 1) banyaknya kuota internet yang dihabiskan dalam sebulan (dalam GB), 2) penghasilan per bulan (dalam juta Rupiah), dan 3) penggunaan bensin yang digunakan untuk transportasi per bulan (liter). Misalkan hasil sampling tersebut diringkaskan dalam tabel berikut.
Data tersebut dapat disajikan dalam bentuk matriks X sebagai berikut.
Secara umum, data yang diambil dari n buah sampel dengan masing-masing p buah variabel pada setiap sampelnya dapat dinyatakan dalam suatu matriks X berukuran n x p sebagai berikut.
Setiap baris dari X merupakan suatu pengamatan multivariat (multivariate observation).
Rata-rata setiap variabel dapat diperoleh dari matriks rata-rata sebagai berikut:
dengan 1n adalah matriks baris dengan n buah kolom, yang semua elemennya bernilai 1. Jadi, matriks rata-rata untuk data di atas adalah:
Dari matriks rata-rata tersebut dapat diketahui bahwa rata-rata penggunaan kuota internet per bulan adalah 120 GB, rata-rata penghasilan per bulan adalah Rp 9 juta, dan rata-rata penggunaan bensin per bulan adalah 22 liter.
Matriks simpangan terhadap rata-rata (T) dapat ditentukan dengan rumus:
dengan I adalah matriks identitas dengan orde n.
Jadi, matriks simpangan untuk data di atas ditentukan sebagai berikut:
Untuk menentukan variansi dan kovariansi sampel, dapat digunakan matriks S sebagai berikut:
Matriks tersebut dapat juga diperoleh dengan:
atau
Jadi, untuk data di atas, diperoleh:
Entri-entri di bagian diagonal S menunjukkan variansi. sii menyatakan variansi Xi (i = 1, 2, 3, …, p).
Jadi, pada matriks S di atas,
s11 = variansi X1 = variansi penggunaan kuota internet per bulan = 4600 GB2
s22 = variansi X2 = variansi penghasilan per bulan = 6,67 (juta Rp)2
s33 = variansi X3 = variansi penggunaan bensin per bulan = 48 liter2
Pada matriks S, untuk , sij menyatakan kovariansi antara Xidan Xj (i, j = 1, 2, 3, …, p). Jadi, pada matriks S di atas,
s12 = kovariansi antara X1 dan X2 = 173,33 GB.(juta Rp)
s13 = kovariansi antara X1 dan X3 = 373,33 GB.liter
s23 = kovariansi antara X2 dan X3 = 13,33 (juta Rp).liter
Koefisien korelasi dapat diperoleh dari matriks korelasi berikut:
dengan menyatakan matriks invers dari , sedangkan matriks itu sendiri didefinisikan sebagai matriks berikut:
Elemen baris ke-i kolom ke-j matriks tersebut bernilai 0 apabila dan bernilai apabila i = j.
Kemudian, dapat ditunjukkan dengan mudah bahwa:
Pada contoh di atas, matriks korelasinya adalah:
Dari matriks tersebut, dapat kita peroleh:
Koefisien korelasi antara X1 dan X2 adalah r12 = 0,9898. Ini adalah koefisien korelasi antara penggunaan kuota internet per bulan dan penghasilan bulanan. Koefisien korelasi antara X1 dan X3 adalah r13 = 0,7945, yaitu korelasi antara penggunaan kuota internet per bulan dan penggunaan bensin dalam sebulan. Koefisien korelasi antara X2 dan X3 adalah r23 = 0,7454. Nilai tersebut merupakan koefisien korelasi antara penghasilan bulanan dengan penggunaan bensin dalam sebulan.
MATRIKS VARIANSI-KOVARIANSI DAN MATRIKS KORELASI
(English version of this article is available at edsmathscholar.com, click here)
Salah satu hal yang perlu dipahami untuk mempelajari statistika multivariat adalah matriks varians-kovarians. Statistika multivariat berhubungan dengan n x p buah data hasil sampling, di mana n adalah banyaknya sampel dan p adalah banyaknya pengukuran yang dilakukan terhadap masing-masing sampel. Sebagai contoh, dilakukan pengukuran terhadap 4 orang sampel penelitian. Kepada setiap sampel tersebut ditanyakan tiga hal, yaitu: 1) banyaknya kuota internet yang dihabiskan dalam sebulan (dalam GB), 2) penghasilan per bulan (dalam juta Rupiah), dan 3) penggunaan bensin yang digunakan untuk transportasi per bulan (liter). Misalkan hasil sampling tersebut diringkaskan dalam tabel berikut.
Data tersebut dapat disajikan dalam bentuk matriks X sebagai berikut.
Secara umum, data yang diambil dari n buah sampel dengan masing-masing p buah variabel pada setiap sampelnya dapat dinyatakan dalam suatu matriks X berukuran n x p sebagai berikut.
Setiap baris dari X merupakan suatu pengamatan multivariat (multivariate observation).
Rata-rata setiap variabel dapat diperoleh dari matriks rata-rata sebagai berikut:
sebagai berikut:
dengan 1n adalah matriks baris dengan n buah kolom, yang semua elemennya bernilai 1. Jadi, matriks rata-rata untuk data di atas adalah:
Dari matriks rata-rata tersebut dapat diketahui bahwa rata-rata penggunaan kuota internet per bulan adalah 120 GB, rata-rata penghasilan per bulan adalah Rp 9 juta, dan rata-rata penggunaan bensin per bulan adalah 22 liter.
Matriks simpangan terhadap rata-rata (T) dapat ditentukan dengan rumus:
Jadi, matriks simpangan untuk data di atas ditentukan sebagai berikut:
Untuk menentukan variansi dan kovariansi sampel, dapat digunakan matriks S sebagai berikut:
Matriks tersebut dapat juga diperoleh dengan:
atau
Jadi, untuk data di atas, diperoleh:
Entri-entri di bagian diagonal S menunjukkan variansi. sii menyatakan variansi Xi (i = 1, 2, 3, …, p).
Jadi, pada matriks S di atas,
s11 = variansi X1 = variansi penggunaan kuota internet per bulan = 4600 GB2
s22 = variansi X2 = variansi penghasilan per bulan = 6,67 (juta Rp)2
s33 = variansi X3 = variansi penggunaan bensin per bulan = 48 liter2
Pada matriks S, untuk , sij menyatakan kovariansi antara Xi dan Xj (i, j = 1, 2, 3, …, p). Jadi, pada matriks S di atas,
, sij menyatakan kovariansi antara Xi dan Xj (i, j = 1, 2, 3, …, p). Jadi, pada matriks S di atas,
s12 = kovariansi antara X1 dan X2 = 173,33 GB.(juta Rp)
s13 = kovariansi antara X1 dan X3 = 373,33 GB.liter
s23 = kovariansi antara X2 dan X3 = 13,33 (juta Rp).liter
Koefisien korelasi dapat diperoleh dari matriks korelasi berikut:
dengan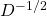 menyatakan matriks invers dari
menyatakan matriks invers dari  , sedangkan matriks
, sedangkan matriks  itu sendiri didefinisikan sebagai matriks berikut:
itu sendiri didefinisikan sebagai matriks berikut:
Elemen baris ke-i kolom ke-j matriks tersebut bernilai 0 apabila dan bernilai
dan bernilai 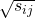 apabila i = j.
apabila i = j.
Kemudian, dapat ditunjukkan dengan mudah bahwa:
Pada contoh di atas, matriks korelasinya adalah:
Dari matriks tersebut, dapat kita peroleh:
Koefisien korelasi antara X1 dan X2 adalah r12 = 0,9898. Ini adalah koefisien korelasi antara penggunaan kuota internet per bulan dan penghasilan bulanan. Koefisien korelasi antara X1 dan X3 adalah r13 = 0,7945, yaitu korelasi antara penggunaan kuota internet per bulan dan penggunaan bensin dalam sebulan. Koefisien korelasi antara X2 dan X3 adalah r23 = 0,7454. Nilai tersebut merupakan koefisien korelasi antara penghasilan bulanan dengan penggunaan bensin dalam sebulan.
Bagikan ini:
Most visitors also read :
PENGUJIAN VALIDITAS KUESIONER DENGAN CARA SEDERHANA
PENDAHULUAN REGRESI LINIER BERGANDA
BERKENALAN DENGAN DISTRIBUSI NORMAL BAKU
BERKENALAN DENGAN REGRESI LINIER SEDERHANA