Di post saya yang lalu, kita mempertanyakan: “Apakah turunan dari y = x5?” Kita jawab: Turunan dari y = x5 adalah y’ = 5x4. Sekarang bagaimana kalau pertanyaannya seperti ini: “Jika y’ = 5x4, maka y = … ?”. Dalam hal ini, kita diminta mencari y sedemikian hingga y’ = 5x4. Dalam “bahasa kalkulus”, ini sama dengan mempertanyakan integral tak tentu dari y’ = 5x4. Apakah y = x5 merupakan jawaban dari pertanyaan tersebut? Belum tentu. Ada tak berhingga banyaknya kemungkinan bagi y. Mungkin saja y = x5 + 8. Mungkin juga y = x5 – 15. Mungkin juga y = x5 + √2. Ketiganya ini menghasilkan y’ = 5x4. Karena itu kita dapat menuliskan jawaban bagi pertanyaan ini sebagai berikut: y = x5 + C, dengan C suatu konstanta. y = x5 + C merupakan suatu antiturunan (atau integral tak tentu) dari y’ = 5x4. Dapat kita tuliskan ∫5x4 dx = x5 + C. Sebelum melanjutkan, kita pelajari terlebih dahulu definisi berikut.
Definisi Antiturunan
F disebut suatu antiturunan f pada selang I jika untuk setiap x ∊ I berlaku F’(x) = f(x).
Catatan:
Jika x merupakan titik ujung interval I, F’(x) yang dimaksud di atas merupakan turunan sepihak.
Nama lain dari antiturunan adalah integral tak tentu (indefinite integrals)
Rumus-rumus Integral Tak Tentu
Perhatikan suatu fungsi f dengan [pmath]f(x) ~=~ 1/{n+1} x^{n+1}[/pmath]. Dengan rumus R1 pada post saya mengenai rumus-rumus turunan, kita dapatkan bahwa f’(x) = xn. Menggunakan definisi antiturunan, kita dapat menuliskan:
…………………………………….. (A1)
dengan n adalah suatu bilangan rasional.
Selanjutnya, karena turunan dari y = x adalah y’ = 1, dapat kita tuliskan:
atau ………………………………………………………….. (A2)
dengan C suatu konstanta.
Sekarang, misalkan y = kx, dengan k merupakan suatu konstanta. Karena y’ = k, definisi antiturunan mengakibatkan kita dapat menyatakan bahwa:
…………………………………………………………… (A4)
Penggunaan rumus (R3) pada post saya yang lalu, untuk c = 1 memberikan hasil . Jadi, menggunakan definisi antiturunan, kita dapat menyimpulkan:
…………………………………………………….. (A5)
Rumus (R11) pada post saya yang lalu menyatakan bahwa . Menggunakan definisi antiturunan, kita dapat menyatakan:
…………………………………………………….. (A6)
Dengan definisi antiturunan, padanan dari rumus (R5) sampai dengan (R10) pada post saya yang lalu dapat dinyatakan sebagai:
[pmath]int{ }{ }{cos x ~ dx} ~=~ sin x[/pmath] …………………………………………………………… (A7)
[pmath]int{ }{ }{sin x ~ dx} ~=~ – ~ cos x[/pmath] ………………………………………………………. (A8)
[pmath]int{ }{ }{sec^2 x ~ dx} ~=~ tan x[/pmath] ………………………………………………………. (A9)
[pmath]int{ }{ }{cosec x ~.~ cot x ~ dx} ~=~ – ~ cosec x[/pmath] ………………………………… (A10)
[pmath]int{ }{ }{sec x ~.~ tan x ~ dx} ~=~ sec x[/pmath] …………………………………………… (A11)
INTEGRAL TAK TENTU (INDEFINITE INTEGRALS) – (1)
Di post saya yang lalu, kita mempertanyakan: “Apakah turunan dari y = x5?” Kita jawab: Turunan dari y = x5 adalah y’ = 5x4. Sekarang bagaimana kalau pertanyaannya seperti ini: “Jika y’ = 5x4, maka y = … ?”. Dalam hal ini, kita diminta mencari y sedemikian hingga y’ = 5x4. Dalam “bahasa kalkulus”, ini sama dengan mempertanyakan integral tak tentu dari y’ = 5x4. Apakah y = x5 merupakan jawaban dari pertanyaan tersebut? Belum tentu. Ada tak berhingga banyaknya kemungkinan bagi y. Mungkin saja y = x5 + 8. Mungkin juga y = x5 – 15. Mungkin juga y = x5 + √2. Ketiganya ini menghasilkan y’ = 5x4. Karena itu kita dapat menuliskan jawaban bagi pertanyaan ini sebagai berikut: y = x5 + C, dengan C suatu konstanta. y = x5 + C merupakan suatu antiturunan (atau integral tak tentu) dari y’ = 5x4. Dapat kita tuliskan ∫5x4 dx = x5 + C. Sebelum melanjutkan, kita pelajari terlebih dahulu definisi berikut.
Definisi Antiturunan
F disebut suatu antiturunan f pada selang I jika untuk setiap x ∊ I berlaku F’(x) = f(x).
Catatan:
Rumus-rumus Integral Tak Tentu
Perhatikan suatu fungsi f dengan [pmath]f(x) ~=~ 1/{n+1} x^{n+1}[/pmath]. Dengan rumus R1 pada post saya mengenai rumus-rumus turunan, kita dapatkan bahwa f’(x) = xn. Menggunakan definisi antiturunan, kita dapat menuliskan:
dengan n adalah suatu bilangan rasional.
Selanjutnya, karena turunan dari y = x adalah y’ = 1, dapat kita tuliskan:
atau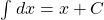 ………………………………………………………….. (A2)
………………………………………………………….. (A2)
dengan C suatu konstanta.
Sekarang, misalkan y = kx, dengan k merupakan suatu konstanta. Karena y’ = k, definisi antiturunan mengakibatkan kita dapat menyatakan bahwa:
Penggunaan rumus (R3) pada post saya yang lalu, untuk c = 1 memberikan hasil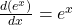 . Jadi, menggunakan definisi antiturunan, kita dapat menyimpulkan:
. Jadi, menggunakan definisi antiturunan, kita dapat menyimpulkan:
Rumus (R11) pada post saya yang lalu menyatakan bahwa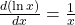 . Menggunakan definisi antiturunan, kita dapat menyatakan:
. Menggunakan definisi antiturunan, kita dapat menyatakan:
Dengan definisi antiturunan, padanan dari rumus (R5) sampai dengan (R10) pada post saya yang lalu dapat dinyatakan sebagai:
[pmath]int{ }{ }{cos x ~ dx} ~=~ sin x[/pmath] …………………………………………………………… (A7)
[pmath]int{ }{ }{sin x ~ dx} ~=~ – ~ cos x[/pmath] ………………………………………………………. (A8)
[pmath]int{ }{ }{sec^2 x ~ dx} ~=~ tan x[/pmath] ………………………………………………………. (A9)
[pmath]int{ }{ }{cosec x ~.~ cot x ~ dx} ~=~ – ~ cosec x[/pmath] ………………………………… (A10)
[pmath]int{ }{ }{sec x ~.~ tan x ~ dx} ~=~ sec x[/pmath] …………………………………………… (A11)
[pmath]int{ }{ }{cosec^2 x ~ dx} ~=~ – ~ cot x[/pmath] …………………………………………….. (A12)
Padanan rumus (R4):
Note: Pada (A13), a > 0
(bersambung)
Lihat juga materi lain terkait integral tak tentu:
Teknik integrasi fungsi trigonometri (1)
Teknik integrasi fungsi trigonometri (2)
Rumus-rumus reduksi integral fungsi trigonometri
Bagikan ini:
Most visitors also read :
BERKENALAN DENGAN NILAI DAN VEKTOR EIGEN
DEKOMPOSISI NILAI SINGULAR (SINGULAR VALUE DECOMPOSITION)
MATRIKS AKAR KUADRAT
SOAL DAN PEMBAHASAN ANALISIS KOMPONEN UTAMA